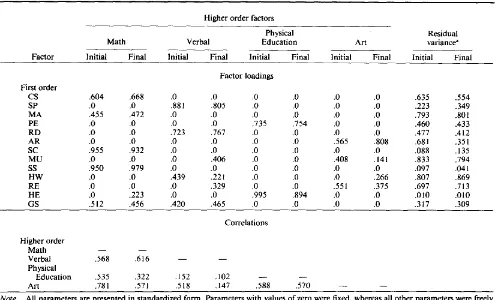
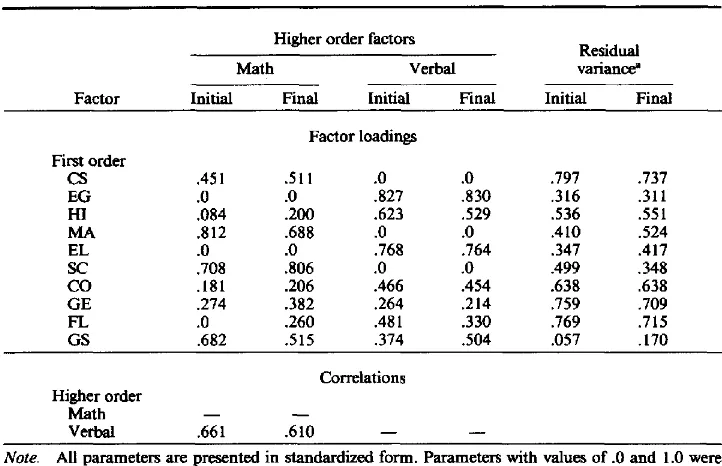
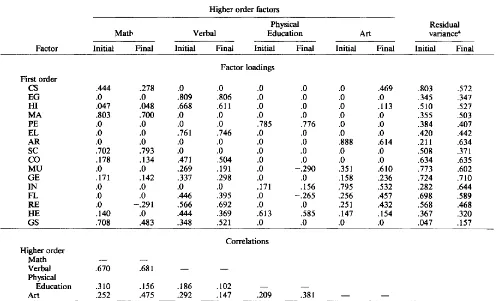
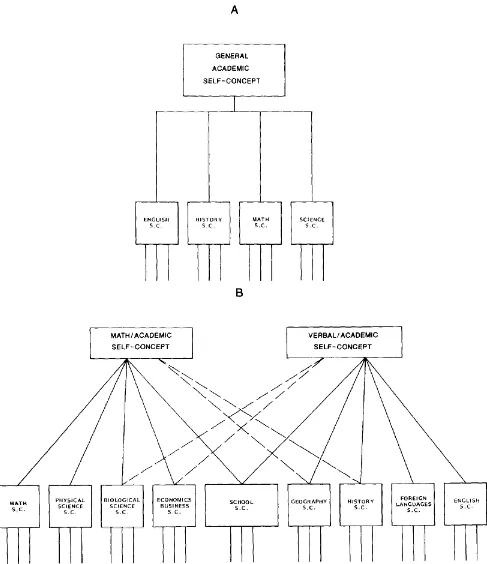
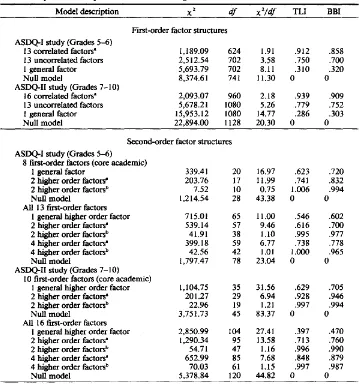
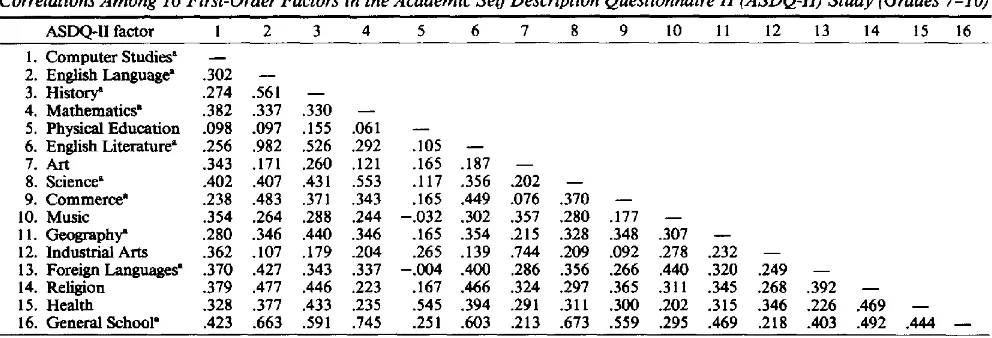
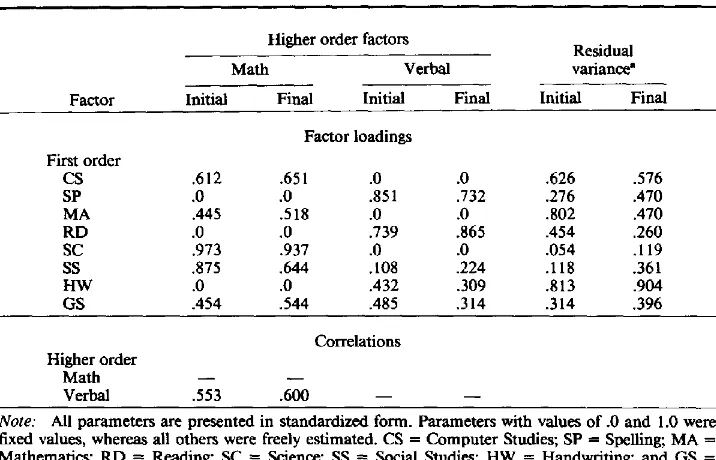
STRUCTURE OF ACADEMIC SELF-CONCEPT
Teks penuh
Gambar
Garis besar
Dokumen terkait
SISTEM KOORDINASI PEMBANGKITAN HYDRO-THERMAL DENGAN MEMPERHITUNGKAN RUGI- RUGI TRANSMISI BERBASIS ALGORITMA GENETIKA.. Universitas Pendidikan Indonesia | repository.upi.edu |
Jika kemudian hari terbukti bahwa karya saya ini bukan hasil asli saya atau merupakan jiplakan dari karya orang lain, maka saya bersedia menerima sanksi
8 Merunut kekerabatan makhluk hidup berdasarkan pohon filogenetiknya Klasifikasi dan Philogeni Deduktif : Ceramah, Tanya-jawab. A:
Penelitian ini bertujuan untuk menguji dan menganalisis pengaruh nilai pelanggan terhadap kepuasan serta dampak kepuasan terhadap loyalitas pelanggan Metro Supermarket Medan
Pada kasus ini, kami melaporkan perawatan oligodontia memakai mahkota akrilik untuk gigi anterior rahang atas dan bawah serta pembuatan gigi tiruan lepasan untuk rahang bawah untuk
Sehubungan butir 1 (satu) diatas, maka Saudara diundang untuk mengadakan Klarifikasi dan Negosiasi Teknis dan Biaya Pekerjaan Pengadaan Suku Cadang Kapal Pangkalan PLP Kelas I I
untuk belajar di dalam kelas. Kurikulum yang dipakai antara siswa tunanetra dengan siswa.. reguler pun sama. Begitupun pendekatan yang dipergunakan
Berdasarkan hal tersebut kami melakukan penelitian ini untuk melihat manfaat kombinasi HD/HP terhadap bersihan molekul, sedang dan besar racun uremik pada