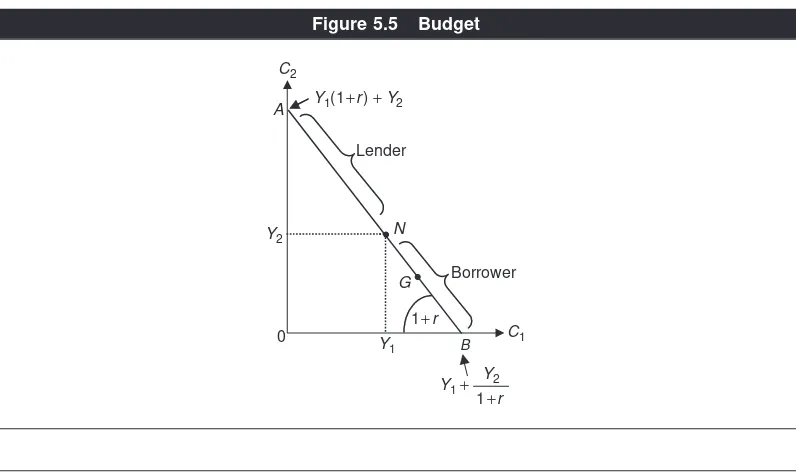
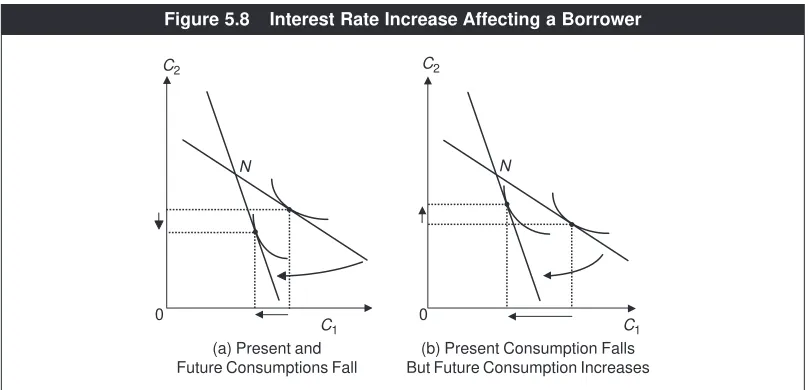
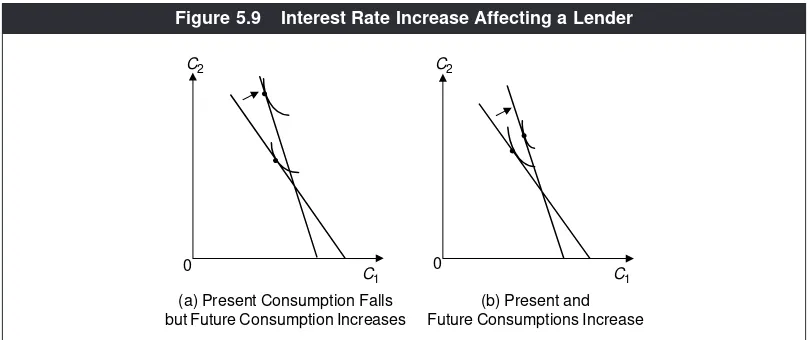
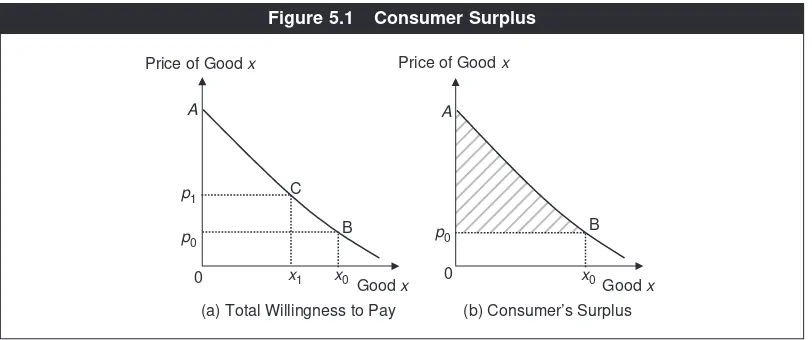
Applications of Consumer Theory
Teks penuh
Gambar
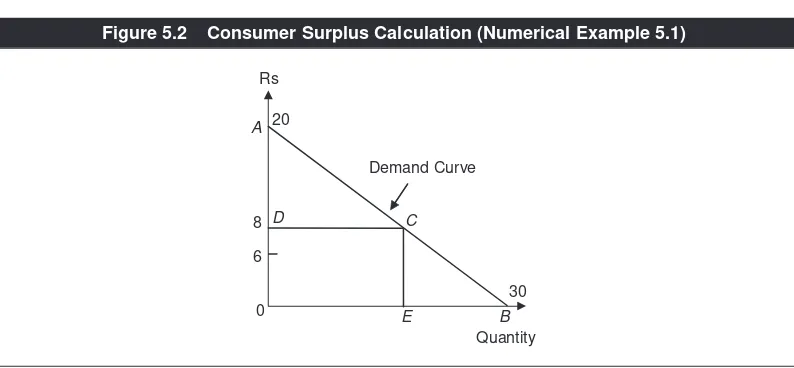
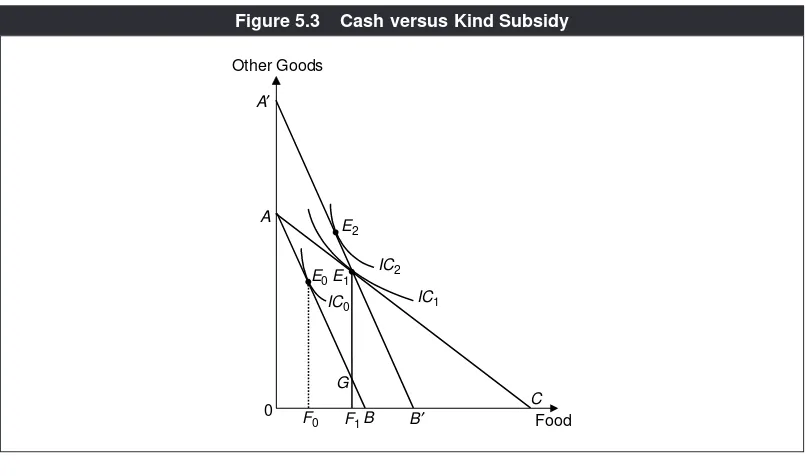
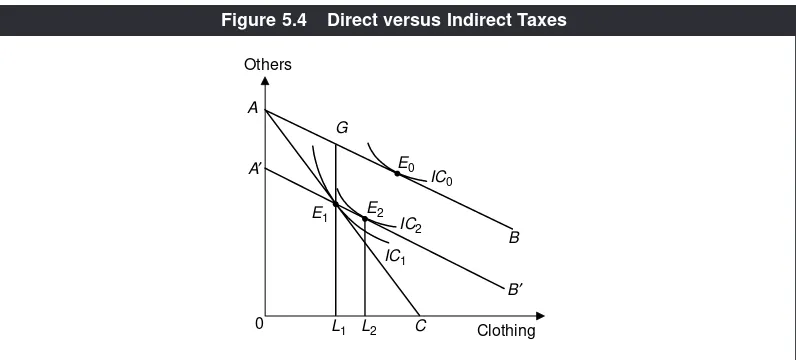
Garis besar
Dokumen terkait
525 Galih Rizki Wahyudhi Inovasi Alat Pengering Ikan dengan Energi Mandiri Guna Meningkatkan Produktivitas Accen Corporation Institut Teknologi Sepuluh Nopember PKMT. 526 Achmad
untuk unsur katoda tersebut. Berkas sinar yang diemisikan bergerak melalui nyala dan berkas dengan λ tertentu yang dipilih dengan monokromator akan diserap oleh uap atom
Kurikulum Standard Sekolah Rendah (KSSR) Pendidikan Khas (Masalah Pembelajaran) dibina selaras dengan Falsafah Pendidikan Kebangsaan yang berlandaskan prinsip-prinsip
.Belajar adalah Rahmat ; Aku belajar tulus penuh rasa syukur 2.. Belajar adalah panggilan ; Aku belajar tuntas penuh
Landasan sosiologis pendidikan toleransi di pesantren adalah bahwa pluralitas agama dan paham keagamaan merupakan realitas hidup dan menjadi social capital yang
Sistem pemeliharaan kambing di Indonesia sebagian besar masih tradisional, termasuk pola pemeliharaan dan pakan yang diberikan.Kebiasaan pemberian hijauan sebagai
[r]
Secara umum nilai rerata pertumbuhan menurut jenis pakan pada semua tingkatan ransum harian terlihat bahwa ikan rucah memberikan hasil lebih baik dibandingkan dengan dua jenis