Abstract: This study aims to describe the attainment of mathematical problem solving ability
Teks penuh
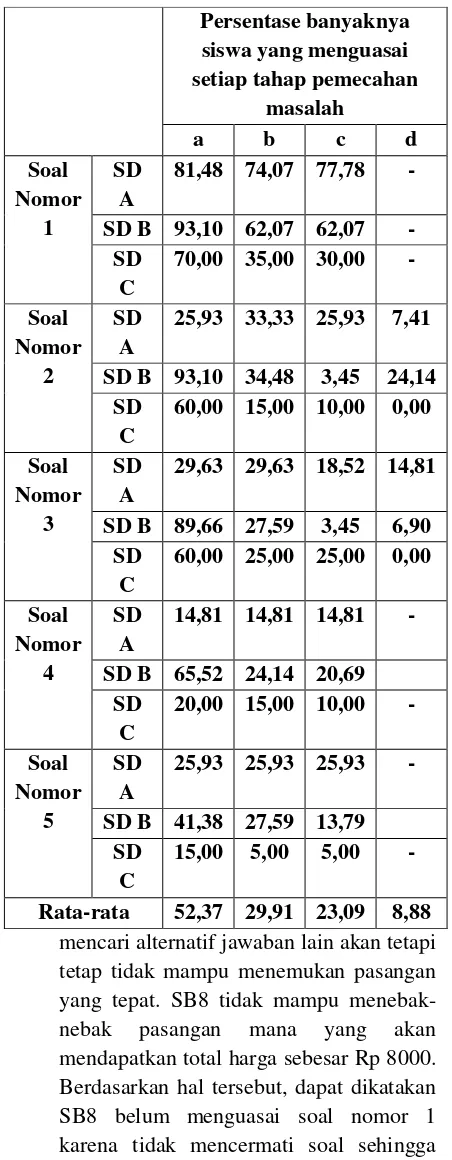
Gambar



Dokumen terkait
Sedangkan variabel workload tidak berpengaruh terhadap kualitas audit pada Kantor Akuntan Publik big four dan non big four yang berafiliasi hal ini diduga lebih
Selama ini subyek sengketa masih belum jelas, seperti belum menetapkan secara tegas bahwa apakah penyelenggara Pemilu baik KPU sebagai penyelenggara Pemilu maupu Bawaslu
Peningkatan kekuatan mekanik material sebesar 24% dibandingkan dengan material tanpa penmabahan nanopartikel, ini terjadi pada penambahan fraksi massa SiO 2 sebesar 0,0087.
Dengan memiliki pelanggan- pelanggan yang setia berarti perusahaan atau organisasi bisnis memiliki mitra bisnis yang sangat potensial untuk keberlangsungan jalannya bisnis perusahaan
Pelajari cara untuk menentukan target pasar Anda dalam minggu-minggu ini dari buku-buku bisnis untuk memulai langkah utama dalam melakukan branding yang baik2. Kelola dan
Pedoman standar gedung kantor Komisi Pemilihan Umum, Komisi Pemilihan Umum Provinsi, Komisi Independen Pemilihan Provinsi, Komisi Pemilihan Umum Kabupaterr/Kota dan
Menyatakan dengan sesungguhnya bahwa hasil skripsi saya yang berjudul : PENYESUAIAN DIRI REMAJA PUTRI YANG TINGGAL DI KOST TERHADAP DUKUNGAN SOSIAL ORANGTUA.. Benar-benar
Hal ini dilakukan dengan cara pengujian variabel upah minimum regional, investasi, pertumbuhan ekonomi secara parsial, digunakan untuk mengetahui signifikansi dan pengaruh