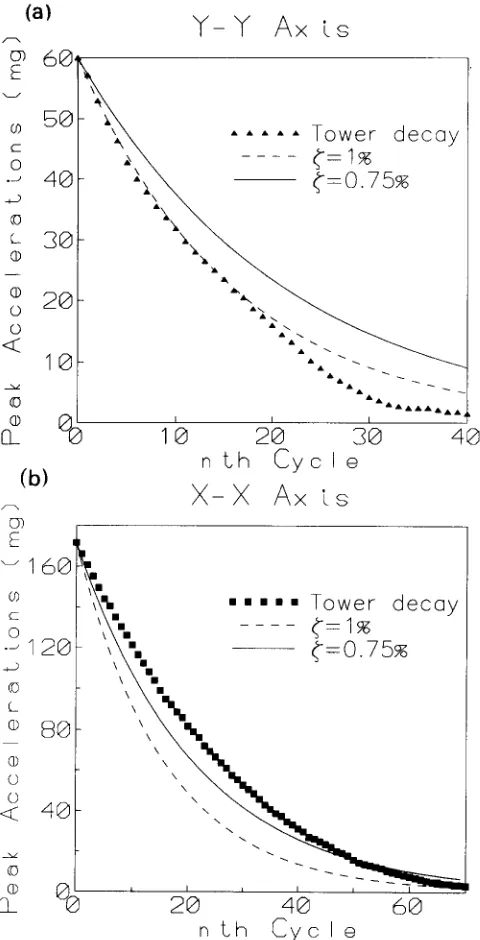
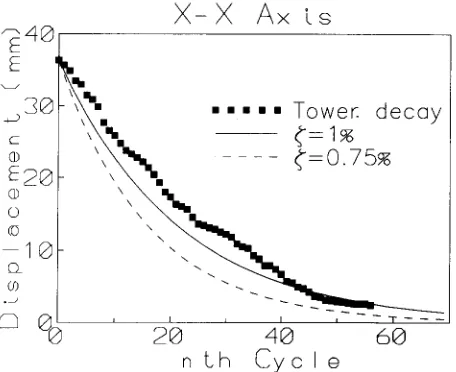
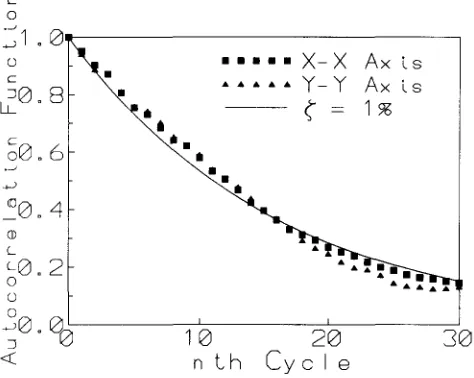
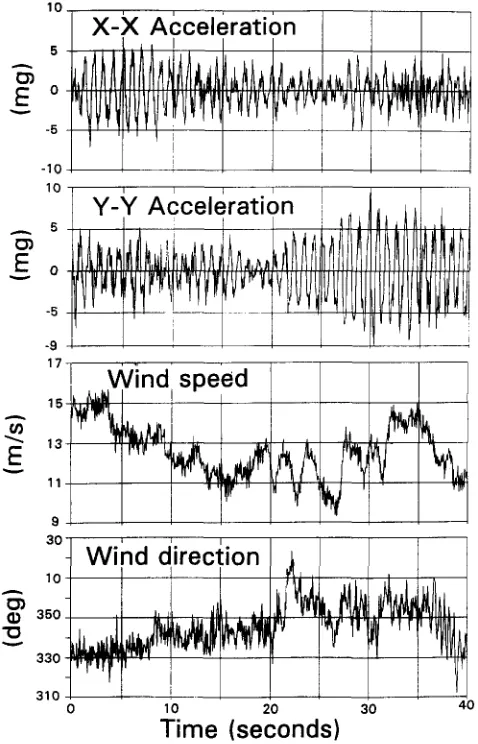
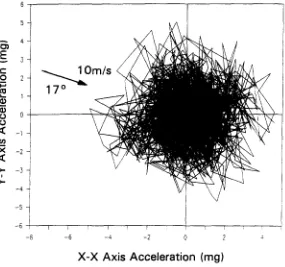
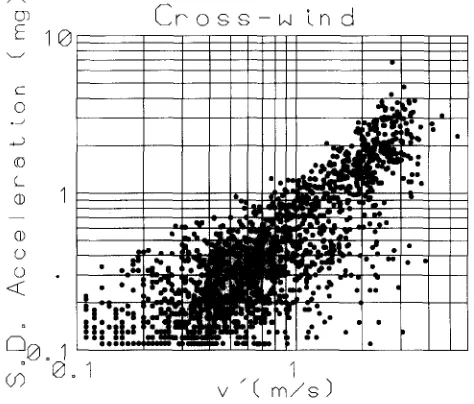
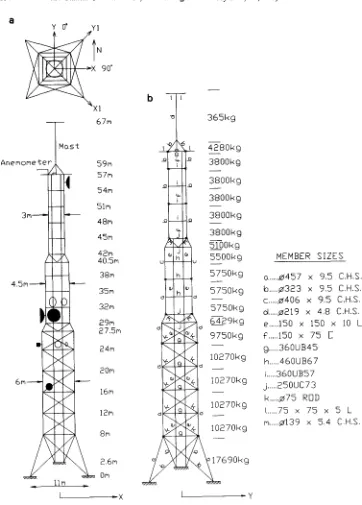
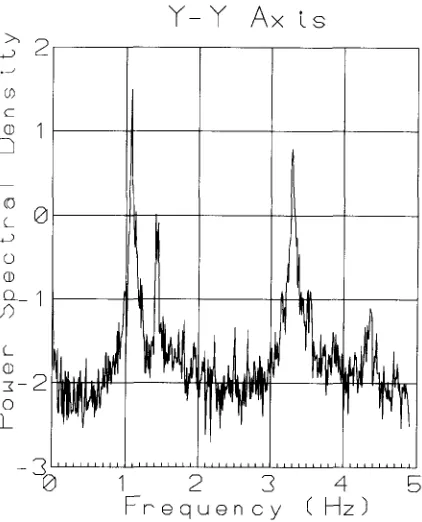
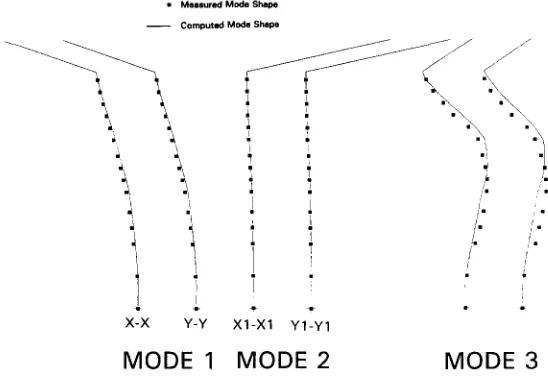
D y n a m i c characteristics and wind induced response of a steel frame tower
Teks penuh
Gambar

Dokumen terkait
PENGEMBANGAN PEMBELAJARAN DI LUAR KELAS MELALUI PROJECT BASED LEARNING DALAM MENINGKATKAN KETERAMPILAN BERPIKIR KREATIF PADA MATERI PENANGANAN LIMBAH. Universitas
Bahwa dalam rangka kelancaran kegiatan Penyust na r Proposal Flibah Peralatan Laboratorium Media Pembelajaran Fakultas Ihnu Keola.'rap,aan (FIK) Universitas Negeri Yogyakarta
Saat lomba Fungsi Mesin Distributing Station dapat berubah (tergantung peralatan yang disediakan)... Fungsi station diuji dengan
PANITIA SELEKSI UMUM DAN LELANG UMUM DINAS PERHUBUNGAN Kota Bekasi 2012. 1 Jun
Kelompok kerja Bagian Layanan Pengadaan Barang Jasa, telah melaksanakan tahapan Pemberian Penjelasan (Aanwijzing) Dokumen Pengadaan dengan metode tanya jawab secara elektronik
Penelitian ini dilatarbelakangi oleh kinerja Penyuluh Lapangan Keluarga Berencana di Desa Sirnabaya Kecamatan Rajadesa masih ada pemahaman masyarakat mengenai program
Berdasarkan Penetapan Pemenang Pelelangan Pekerjaan Pengadaan Perangkat Pengolah Data Biro Keuangan dan Perlengkapan Nomor : 22/Pokja 11/SETJENTAN/5/2012 tanggal 3 Mei
Bila mana pihak saudara tidak hadir pada waktu yang ditentukan diatas tanpa pemberitahuan secara resmi ke kami, maka kami anggap pihak saudara (CV. AN-NAHL)