PENGARUH STRATEGI REACT TERHADAP KEMAMPUAN PEMECAHAN MASALAH MATEMATIS BAGI SISWA KELAS VIII SMP N 3 PABELAN KABUPATEN SEMARANG Nur Laelatunnajah
Teks penuh
Gambar

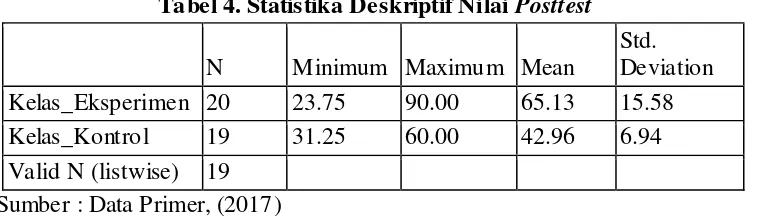
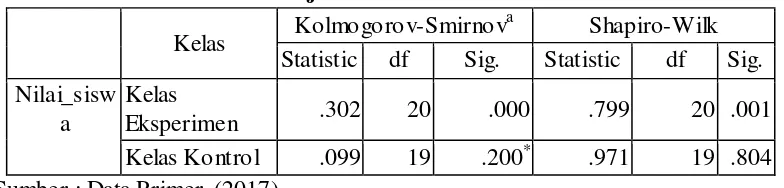

Dokumen terkait
On top of this approach, a reusable tool has been created to provide test models which can be performed against the data provision web services of the Aviation Architecture.
Pada modul versi 2 ini sistem mampu mengelola data blok, mengelola data mata kuliah penawaran, melakukan generate sesi blok, melakukan generate jadwal blok, dan
Data hasil penelitian dianalisis dengan menggunakan teknik korelasi Product Moment dari Carl Pearson , hasilnya menunjukkan bahwa ada hubungan antara stres kerja pada
Silika Amorphous yang dihasilkan dari abu sekam padi diduga sebagai sumber penting untuk menghasilkan silikon murni, karbit silikon, dan tepung nitirit silikon (Katsuki et al
Dana Alokasi Khusus (DAK) adalah dana yang bersumber dari pendapatan APBN yang dialokasikan kepada daerah tertentu dengan tujuan untuk membantu mendanai kegiatan khusus yang
Selanjutnya label sebagai fungsi pemenuhan peraturan perundang- undangan, memiliki konsekuensi bahwa hal yang tercantum pada label harus sesuai dengan kandungan bahan pangan
Program simulasi ini akan menampilkan lima buah band pass filter (BPF) dan program akan menghitung koefisien filter dari pemberian sinyal masukanx. Perhitungan koefisien
Governance as a socio cybernetic system , artinya dampak hasil kepemerintahan (kebijakan pemerintah) bukanlah produk dari apa yang dilakukan (tindakan )