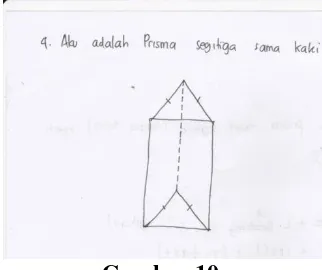
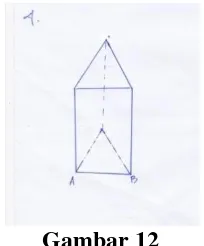
KEMAMPUAN PENALARAN MATEMATIS SISWA KELAS VIII SMP NEGERI 01 SELAKAU
Teks penuh
Gambar
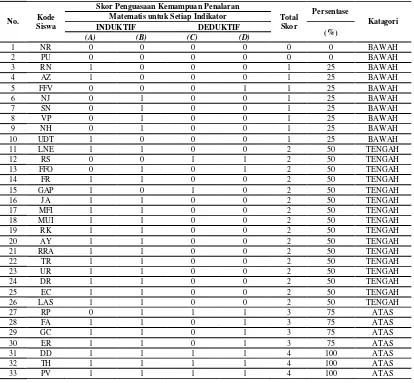
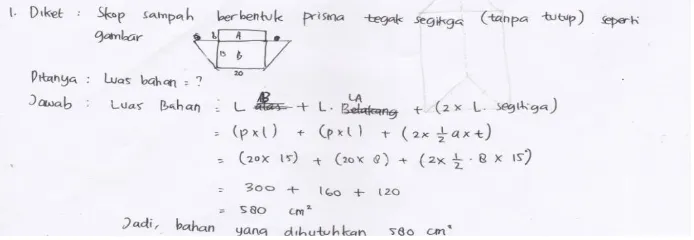

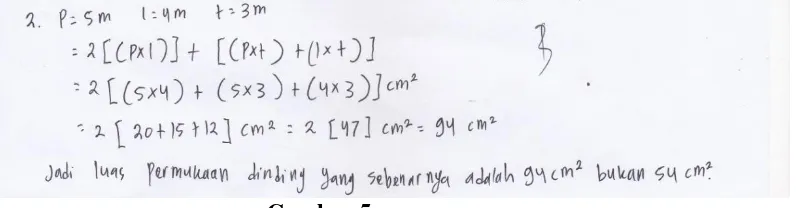
Dokumen terkait
During the training the author did the research entitled: “ DETERMINATION OF ANTIOXIDANT ACTIVITY AND BETALAIN PIGMENT OF FREEZE DRIED RED BEET ( BETA VULGARIS
Tujuan penelitian ini yaitu untuk mengevaluasi penggunaan antibiotika profilaksis pada pasien yang menjalani operasi sesar pada bulan Agustus dan September 2007 di RS
Lampiran I Perhitungan Konversi Satuan Kemiringan Tebing Galian Lampiran J Perhitungan Persentase Kerusakan Jalan. Lampiran K Perhitungan Parameter Kerusakan Lahan Lampiran
Keterkaitan antara variable STU (X 1 ), BRINETS (Variabel X 2 ) sebagai sistem dan variable Kinerja Karyawan (Variabel Y), dapat dilihat pada jurnal Pengaruh
Bagaimanakah kualitas media laboratorium virtual berbasis inkuiri terstruktur pada materi titrasi asam basa dalam meningkatkan keterampilan proses sains dan hasil
Berdasarkan permasalahan diatas, maka Universitas Pancasila khususnya Fakultas Teknik berniat menyelenggarakan seminar berskala nasional yang bertujuan untuk
Tim peneliti melakukan refleksi terhadap pelaksanaan siklus kedua dan menganalisis untuk membuat kesimpulan atas pelaksanaan pembelajaran dengan metode belajar kelompok
Disajikan beberapa pernyataan perilaku dalam kehidupan sehari-hari, peserta didik dapat mengidentifikasi sikap terpuji yang sesuai dengan kandungan