Complex Networks Principles, Methods and Applications pdf pdf
Teks penuh
Gambar


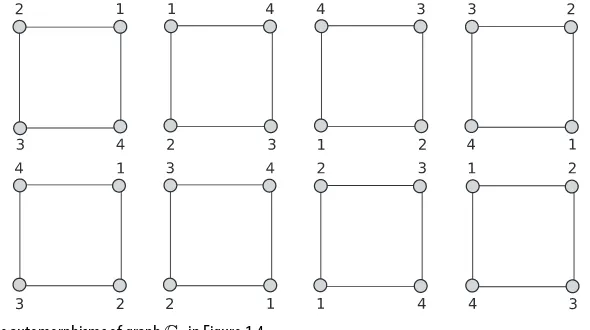
Dokumen terkait
• Together with the chemical variety, a large spectrum of physically different devices based on organic materials is possible and has been developed in the years, the most
Complete access to data, information about the data values, and information about the organization of the data is achieved through a technique herein referred to as introspection
Environmental Research and Public Health Article Combining Monte Carlo Simulation and Bayesian Networks Methods for Assessing Completion Time of Projects under Risk Ali Namazian1,* ,
To make it short, physicists are now applying concepts from Statistical Physics, such as, the ideas of universality, scaling, game theory, networks and agent interaction models, to
Test Methods UPV SWT AE DU CWI Technical points Dependent on environmental effects, Partially closed crack Minimum size of specimen Threshold, Fracture process Variability of
vi Abstract This study investigates and examines the advantages and forecasting performance of combining the dynamic factor model DFM and artificial neural networks ANNs leading to
[34] 2020 Enhance the accuracy and reliability of spectrum sensing in cognitive radio networks by using a MIMO system to combine the sensing information from multiple SUs
In this thesis, we introduced a composite modeling language based on hybrid bond graphs, where we employ an extended version of the Grafcet formalism to model the computation elements