Perencanaan sistem drainase kawasan perumahan Green Mansion Residence Sidoarjo - ITS Repository
Teks penuh
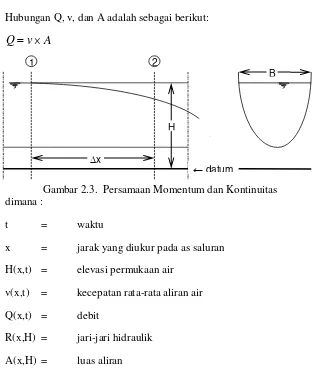
Gambar

Dokumen terkait
Koska voidaan pitää mahdollisena, että tulevaisuudessa myös Suomen ilmavoimat osallistuu kansainvälisiin kriisinhallintaoperaatioihin esimerkiksi ilmatilan valvonnan osalta,
Contoh implementasi paragraf 19 adalah ketika entitas pada periode sebelumnya menyimpang dari suatu ketentuan dalam suatu PSAK untuk pengukuran aset atau laibilitas dan
Puji dan syukur kami panjatkan kehadirat Tuhan Yang Maha Esa, karena berkat rahmat dan hidayahNya serta kerja keras tim penyusun telah berhasil menyusun sebanyak
Hal ini menunjukan bahwa hasil belajar yang diperoleh pada kelas eksperimen lebih baik dibanding pada kelas kontrol, sehingga hal tersebut membuktikan bahwa terdapat perbedaan
Perlakuan komposisi media tanam yang berbeda, memberikan pengaruh nyata pada parameter tinggi tanaman dan jumlah daun, tetapi tidak berpengaruh nyata pada
dari tahun 2005 sampai dengan 2014 Alat analisis yang digunakan dalam penelitian ini adalah analisis regresi linier berganda Dalam pengujian secara simultan,
b. SMP, SMPLB, SMA, SMALB, dan SMK, sesuai dengan yang tercantum pada Ijazah yang diperoleh dari jenjang pendidikan sebelumnya, atau sesuai akte kelahiran/dokumen
Fokus refleksi pada pendekatan guru dalam proses pembelajaran dan hubungannya dengan hasil belajar sementara siswa. Dalam pembelajaran siklus I terdapat