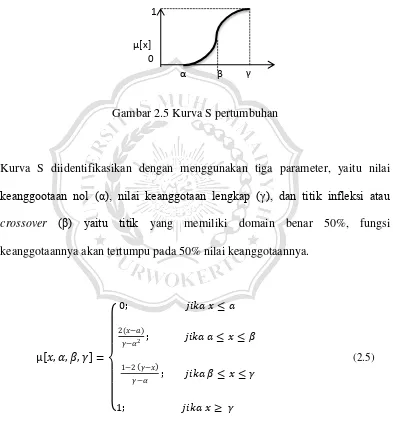
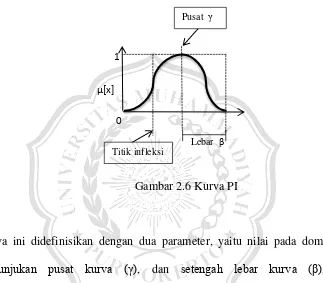
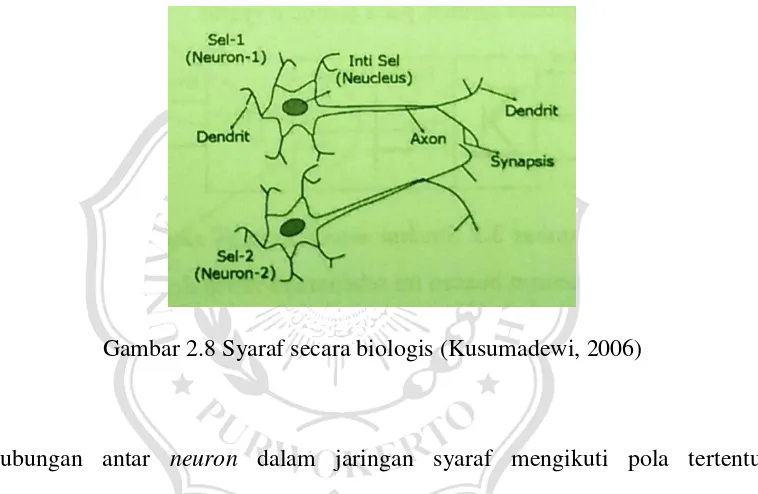
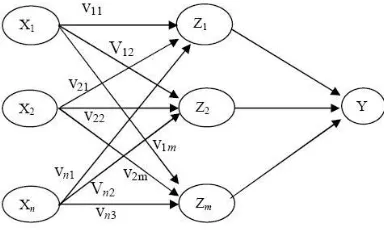
BAB II TINJAUAN PUSTAKA DAN LANDASAN TEORI 2.1 Tinjauan Pustaka - BAB II MUHAMMAD IMAM SETIAJI TI'17
Teks penuh
Gambar


Dokumen terkait
(2006), “Analisis faktor psikologis konsumen yang mempengaruhi keputusan pembelian roti merek Citarasa di Surabaya”, skripsi S1 di jurusan Manajemen Perhotelan, Universitas
Berdasarkan hasil fraksinasi dan analisis dengan kromatografi lapis tipis menunjukkan bahwa hasil isolasi zat aktif senyawa rutin dari madu terdapat hanya pada fraksi
Perancangan website pemetaan lokasi UMKM Kabupaten Musi Banyuasin menggunakan website design method ini memiliki 5 (lima) menu inti untuk admin yaitu kecamatan,
Pengembangan “Model Praksis Gerakan” depan sangat penting atas beberapa alasan dan tujuan: (1) Pengalaman lapangan dan fakta menunjukkan sejumlah kreasi gerakan atau program
ADLN Perpustakaan Universitas Airlangga.. Skripsi ANALISIS FAKTOR
Sesuai dengan kriteria diterima atau ditolaknya hipotesis maka dalam hal ini dapat disimpulkan bahwa menerima hipotesis yang diajukan terbukti atau dengan kata lain variabel
Dapat juga dikemukakan bahwa layanan ini bertujuan untuk membimbing seluruh siswa agar (a) memiliki kemampuan untuk merumuskan tujuan, perencanaan, atau pengelolaan
Dari hasil pengujian blackbox dapat menunjukkan bahwa sistem pendukung keputusan penentuan lokasi pembangunan SPBU menggunakan metode SAW di Kabupaten Merauke