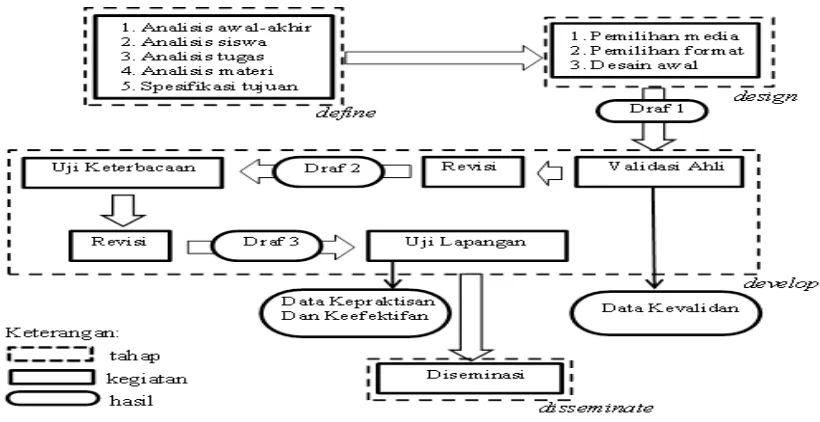
Pengembangan Lembar Kegiatan Siswa (LKS) bangun ruang sisi datar berbasis PBL.
Teks penuh
Gambar


Dokumen terkait
Dalam buku ini juga terpetakan kategori eksistensi etnis Tionghoa berdasarkan wilayah dan sub etnis, yaitu : (1) daerah pesisiran sub-etnis Jawa (Arek) dari sisi
Penelitian hanya akan membahas tentang masalah psikologis yang berkaitan dengan struktur kejiwaan manusia yang didalamnya termasuk Id, Ego, dan Super Ego yang masing-masing
Artikel ini merupakan tesis penulis dalam rangka menyelesaikan studi S2 di MAP Universitas Diponegoro, Semarang. 2 ) Penulis adalah guru besar, staf pengajar sekaligus ketua
Pembelajaran tematik merupakan pembelajaran baru bagi siswa kelas IV SD Al Amin Cemani, hal tersebut membuat siswa kebingungan. Guru kelas IV B menerapkan metode
Hasil penelitian didapatkan bahwa pasien sebagian besar adalah laki-laki pada usia produktif, didiagnosa TB paru kurang dari 6 bulan sebelum penelitian, memiliki PMO, teratur
Sebelum infeksi Setelah infeksi Sebelum infeksi Setelah infeksi.. sensitif terhadap infeksi bakteri yang sangat virulent. THC berubungan erat dengan kelulushidupan udang
Cipta, 2010), h.. pengetahuan dan teknologi serta mampu mengatasi masalah dalam kehidupan sehari- hari. Pendidikan merupakan kebutuhan manusia yang sangat penting untuk
3. Berdasarkan hasil QSPM prioritas strategi maka strategi terpilih dengan Total Attractiveness Score 15, 550 jadi) strartegi yang harus digunakan adalah strategi