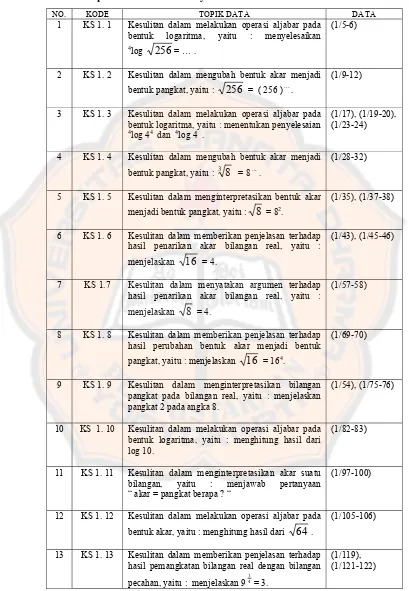
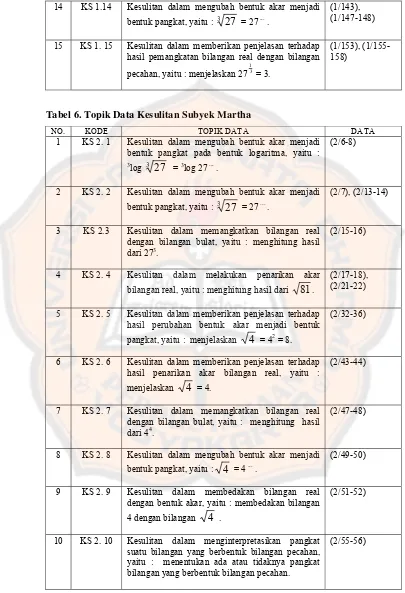
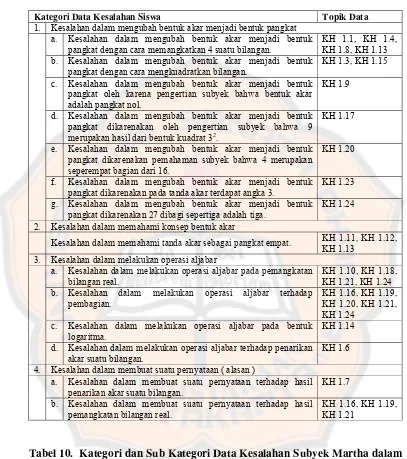
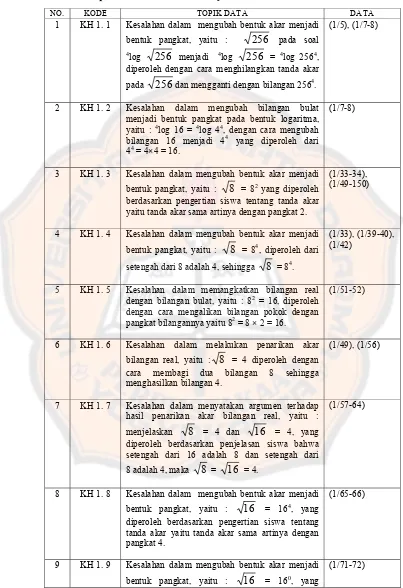
Analisis kesalahan dan kesulitan siswa kelas X SMA Imannuel Kalasan dalam mengubah bentuk akar menjadi bentuk pangkat pada pokok bahasan logaritma.
Bebas
111
0
0
Teks penuh
Gambar



+7
Dokumen terkait