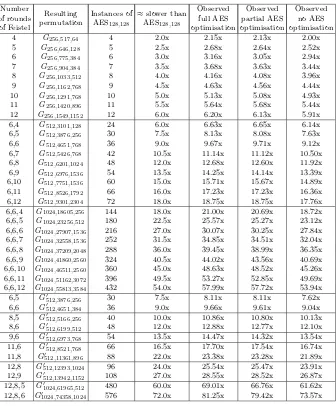
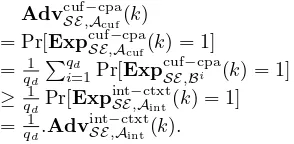Cryptography and Security From Theory to Applications pdf pdf
Teks penuh
Gambar
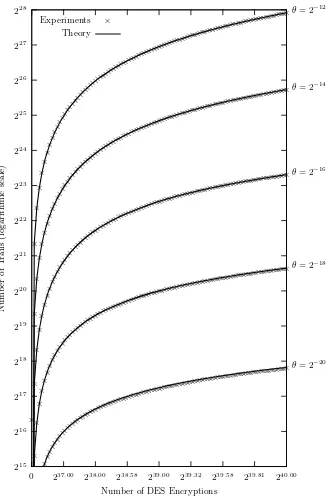
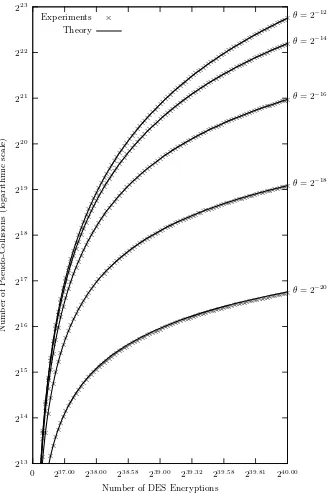
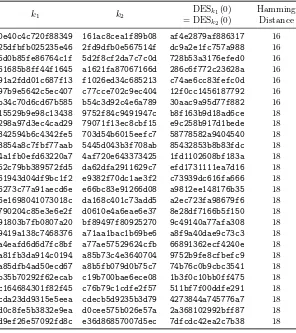
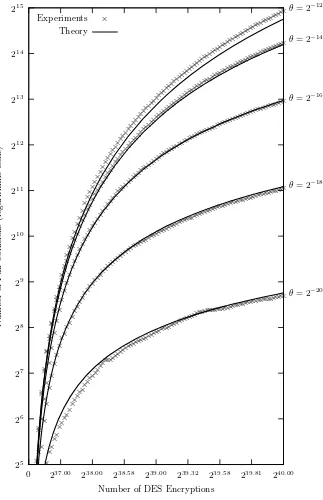
Dokumen terkait
kelas hanya bertumpu kepada murid aliran perdana tanpa melibatkan murid bekas LINUS dan LINUS M1 : Menggalakkan guru melaksanakan PdP mengikut kepelbagaian aras
[r]
20 tahun 2008 pasal 1, usaha kecil adalah usaha ekonomi produktif yang berdiri sendiri, yang dilakukan oleh orang perorangan atau badan usaha yang bukan merupakan anak perusahaan
Dari kaca mata awam hal ini tidak berdampak apapun bagr kehidupan " bahasa terutama bahasa-bahasa kecil Apalagr pemakaian istilah bahasa daerah digunakan dalam
28 Jika investasi lancar dicatat pada metode terendah antara biaya dan nilai pasar, setiap penurunan nilai pasar dan setiap kebalikan dari penurunan tersebut dimasukkan dalam
Oleh karena dalam rangka pemerataan pembangunan, untuk mengurangi ketimpangan dan mengembangkan pembangunan wilayah berdasarkan potensi masing-masing maka pengembangan
Puji dan syukur penulis haturkan ke hadirat Tuhan Yang Maha Esa atas rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi dengan judul “
(2007a) melaporkan bahwa proses SSF lebih toleran terhadap senyawa inhibitor yang terbentuk atau yang berasal dari proses perlakuan penda- huluan, yang biasanya terdapat
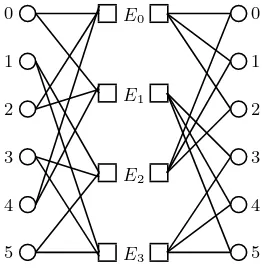
![Fig. 2. Bipartite representation of L[GB2(2, 6, 3, 4)] = GB2(2, 36, 3, 24)](https://thumb-ap.123doks.com/thumbv2/123dok/3934985.1878405/41.429.67.360.53.552/fig-bipartite-representation-l-gb-gb.webp)