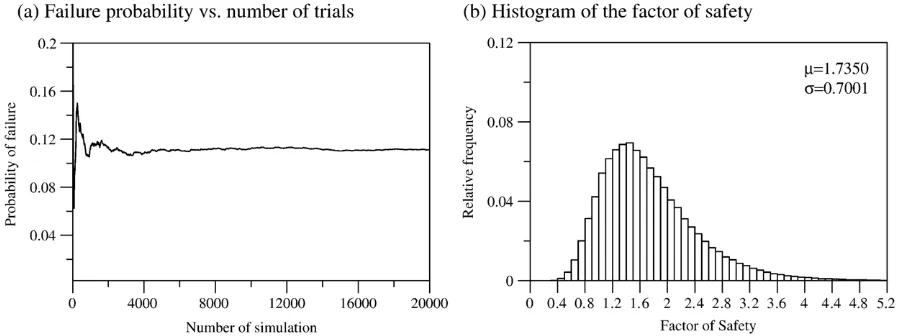
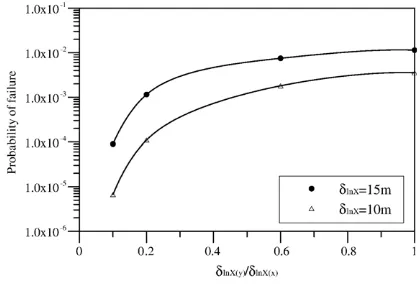
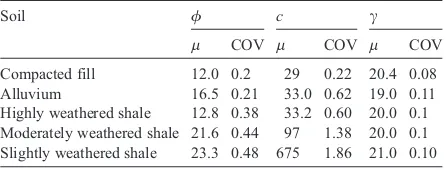
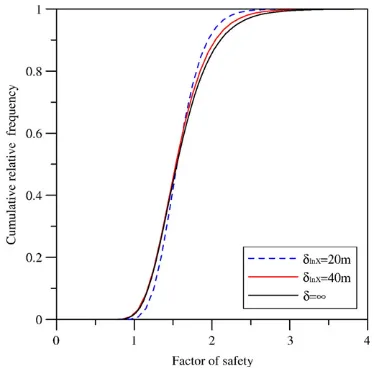
Effects of spatial variability of soil properties on slope stability
Teks penuh
Gambar
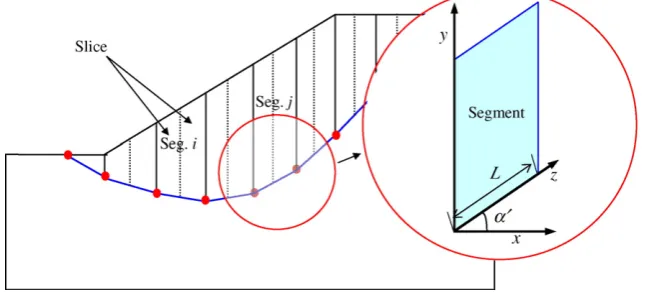

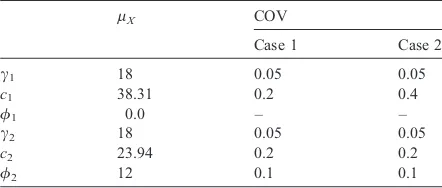

Dokumen terkait
dalam perlindungan dan pengelolaan lingkungan hidup; 17) Meningkatnya kinerja peralatan dan instrumen pengukuran lingkungan. Program BLH Kota Tangerang Tahun 2016 yang
Adanya pengaruh secara simultan yang cukup besar dari faktor-faktor kons- truk diri saling ketergantungan, tingkat pendidikan dan lingkungan pembelajaran
tekan dan analisanya, serta pembahasan persoalan untuk mendapatkan hasil kadar penambahan abu sekam padi yang baik untuk menghasilkan kuat tekan yang optimal namun
Limbah adalah buangan yang dihasilkan dari suatu proses produksi baik industri maupun domestik (rumah tangga), yang kehadirannya pada suatu saat dan tempat
Tipe Pertanyaan, Respon, Dan Praanggapan Yang Muncul Pada Interviu Investigatif Kepolisian.. Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu
Penerapan Peer Assessment Dan Self Assessment Pada Tes Formatif Hidrokarbon Untuk Feedback Siswa SMA Kelas X1. Universitas Pendidikan Indonesia |
[r]
[r]