Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika
Teks penuh
Gambar
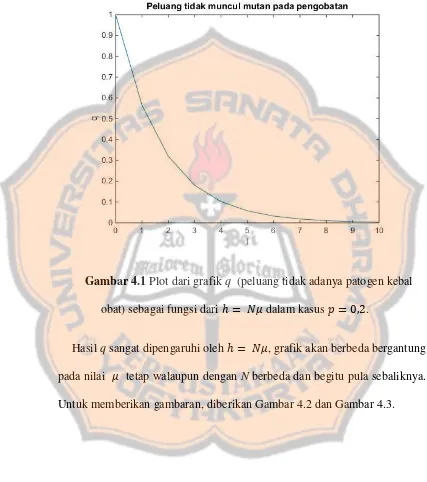


Dokumen terkait
Hasil yang didapat dari penelitian ini adalah: (1) nomogram sebagai sebagai media pembelajaran berhitung matematika sekolah dasar pada materi operasi hitung bilangan bulat
akan dilampirkan program maple yang digunakan untuk menentukan titik kesetimbangan endemik, program metode Runge-Kutta orde empat untuk penyelesaian model matematis
Hasil dari penelitian ini adalah: (1) Langkah-langkah pengembangan modul Matematika yang memfasilitasi peserta didik dalam mengembangkan kemampuan 4C
Mengetahui fitur apa saja yang dapat dimanfaatkan pada Learning Management System (LMS) Google Classroom dalam mendukung pembelajaran matematika kelas VIIIC SMP
Penelitian ini bertujuan untuk mengetahui (1) kemampuan peserta didik kelas VIII B SMP Negeri 1 Yogyakarta dalam menyelesaikan soal matematika tipe HOTs pada
Agnes Theresia Nuhuyanan.. Keefektifan Pembelajaran Matematika dengan Memanfaatkan Aplikasi Edmodo sebagai Media Bantu Diskusi Kelas XI MIPA 4 SMA Negeri 8 Yogyakarta
Adapun batasan masalah dalam penelitian ini adalah cara untuk meningkatkan hasil belajar siswa yang kurang maksimal pada mata pelajaran matematika di SMP Maria Immaculata
Natalia Tatag Hendralita. Analisis Kemampuan Berpikir Kritis Dan Pemecahan Masalah Matematika Dalam Menyelesaikan Soal Cerita Pada Topik Teorema Pythagoras Di