MODEL ANTRIAN DENGAN KEDATANGAN BERDISTRIBUSI POISSON DAN WAKTU PELAYANAN BERDISTRIBUSI ERLANG SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika
Teks penuh
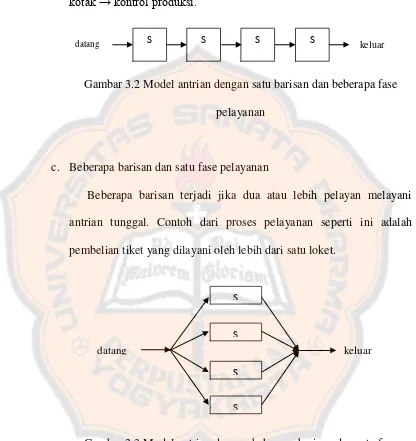
Gambar



Dokumen terkait
1) Identifikasi organisasi dimaksudkan bahwa karyawan bersedia menerima tujuan organisasi yang kemudian dijadikan sebagai dasar untuk mewujudkan komitmen organisasi.
Tujuan dari penulisan ini adalah membuat Sistem Informasi Akademik SMA Immanuel Kalasan berbasis open source dengan menggunakan bahasa pemrograman Gambas dan basis data
Manfaat penulisan ini adalah untuk memahami teknik penyelesaian persamaan Laplace dan persamaan Poisson yang timbul pada masalah aliran panas dua-dimensi dalam pelat persegi
Kepuasan kerja memiliki peran yang sangat penting dalam mengintervening pengaruh kompensasi dan lingkungan kerja terhadap kinerja karyawan dengan tingginya tingkat
Tujuan penulisan skripsi ini adalah untuk mengetahui pengaruh motivasi kerja,disiplin kerja dan komunikasi kerja terhadap kinerja pegawai pada Kantor Dinas
Tujuan penulisan skripsi ini adalah memenuhi gelar Sarjana Akuntansi pada Progam Studi Akuntansi Fakultas Ekonomi Universitas Muhammadiyah Jember.. Peneliti sadar
ANALISIS PERBANDINGAN PENGIRIMAN BARANG MENGGUNAKAN METODE NORTH WEST CORNER DAN LEAST COST.. (STUDI KASUS: PT. COCA COLA AMATIL
Penulisan Skripsi ini membahas tentang “ Hubungan Antara Faktor Pendorong Perilaku Membeli Aksesoris yang Sedang Trend dengan Kepercayaan Diri pada Siswi Jurusan