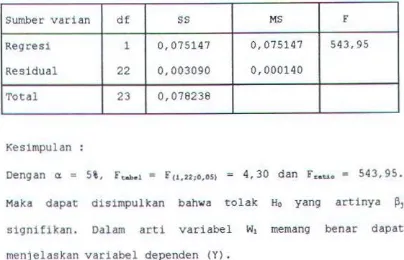
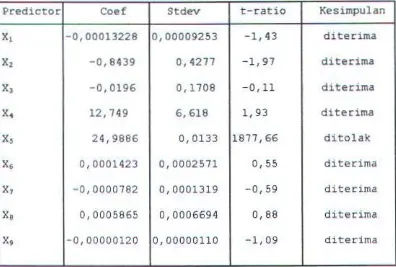
TUGAS AKHIR - Analisis Statistika Terhadap Faktor-Faktor Yang Mempengaruhi Proses Produksi Semen Di PT. Semen Gresik Serta Menduga Fungsi Produksinya - ITS Repository
Teks penuh
Gambar
![Gambar 2.1. Statistik d Durbin Watson [3]](https://thumb-ap.123doks.com/thumbv2/123dok/1754156.2090470/34.613.118.461.93.751/gambar-statistik-d-durbin-watson.webp)

Dokumen terkait
Mengacu pada penelitian yang dilakukan oleh lembaga perusahaan keluarga untuk tinjauan bisnis keluarga, diketahui bahwa hanya 30% dari keseluruhan perusahaan milik keluarga
Personalisasi reward dalam penelitian ini masih terbatas karena menggunakan Finite State Machine yang perilakunya terbatas, sehingga jika dimainkan berulangkali maka
masalah yang terhubung langsung dari PC pengguna SIMRS ke unit TI guna mempersingkat waktu aduan para pengguna dan sekaligus juga dapat menampung aduan terkait
Di Indonesia, yang berdasarkan Pancasila, tidak ada pemisahan sepenuhnya antara negara dan agama, dan bahwa tanggung jawab negara terhadap agama tidak hanya terbatas pada
Selain itu akan terus terjadi kesenjangan yang semakin tinggi dalam struktur masyarakat Indonesia karena para pemilik modal semakin mendapatkan keuntungan yang besar
Penelitian ini bersifat survey dengan pendekatan cross sectional yaitu desain penelitian dengan pengukuran variabel yang dilakukan satu waktu saja untuk mengetahui
Penelitian ini bertujuan untuk mengetahui; (1) perbedaan motivasi belajar siswa kelas X-1 dan X-2 SMA Negeri I Sambi Boyolali dalam pembelajaran ekonomi dengan menggunakan pendekatan
Tapi dulu ketika ada masalah saya memilih untuk diam karena tidak berani untuk bercerita mbak, tapi setelah di sini dan mengenal banyak orang saya lebih berani