PERENCANAAN PENANGGULANGAN BANJIR AKIBAT LUAPAN SUNGAI PETUNG, KOTA PASURUAN, JAWA TIMUR
Teks penuh
Gambar
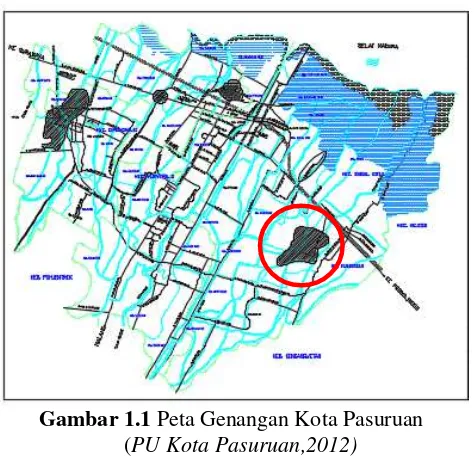
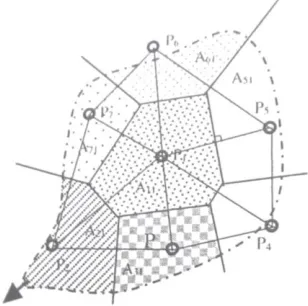


Dokumen terkait
Hukum kedua Newton untuk gerakan translasi menyatakan bahwa jumlah gaya yang bekerja pada suatu benda dalam arah tertentu sama dengan hasil kali massa benda tersebut
Laporan keuangan konsolidasian, disajikan dalam ribuan Rupiah, kecuali dinyatakan lain, telah disajikan dengan metode akrual dan menggunakan konsep biaya perolehan, kecuali
Pada penelitian ini dosis untuk 12 orang pasien anak tersebut ditetapkan sebagai tepat dosis, karena sirup kotrimoksazol yang digunakan sudah mendapatkan ijin edar
Salam dapat diekspresikan melalui ucapan (verbal) dan gerakan (non- verbal) ataupun gabungan keduanya. Pesan verbal dan non verbal yang disampaikan akan mempengaruhi
Sinyal hasil penafsiran dari sensor akan diterima oleh rangkaian amplifier untuk menguatkan sinyal dari sensor, setelah itu masuk ke dalam rangkaian high pass filter yang
Pada penelitian Mirtha Delgado dkk (1999-2001), studi deskriptif di Kuba didapatkan dari 200 pasien (secara acak) di poliklinik Finlay (kota Camaguey), didapatkan hanya 7 kasus
Instalasi ini sangat membantu pihak rumah sakit dalam hal memperbaiki instrumentasi medis atau alat-alat medis yang rusak pada Rumah Sakit Umum Daerah (RSUD) Zainoel Abidin..
Pendapat yang serupa juga dikemukakan oleh Dagun, perbedaan dalam pendidikan antara laki – laki dan perempuan antara lain adalah (1) Perempuan memperoleh skor