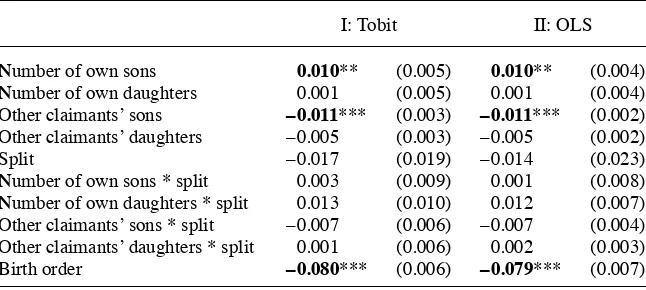
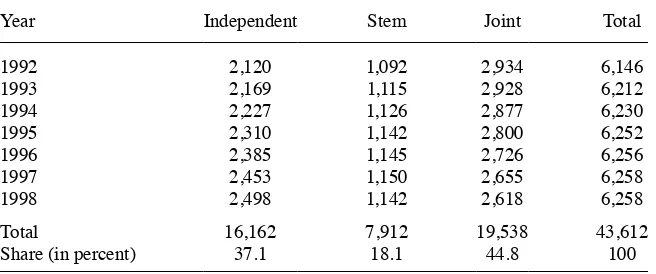
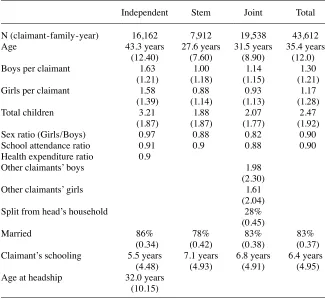
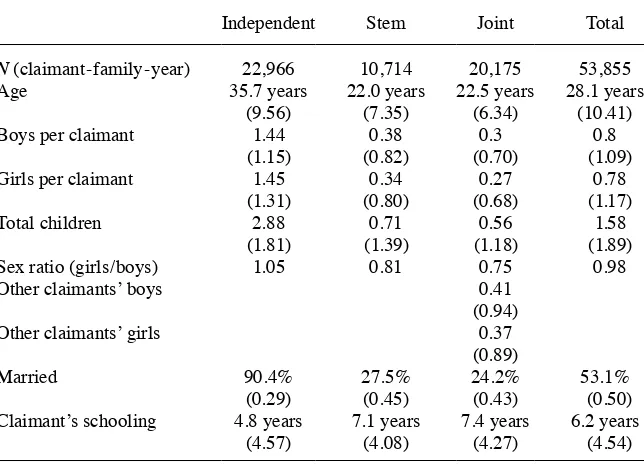
Manajemen | Fakultas Ekonomi Universitas Maritim Raja Ali Haji 393.full
Teks penuh
Gambar
Dokumen terkait
Dengan ini diumumkan Pemenang Seleksi Sedehana dengan metode evaluasi biaya terendah untuk paket pekerjaan sebagaimana tersebut diatas sebagai
Rhegmatogen retinal detachment terjadi karena lubang atropic pada retina atau robekan pada retina yang disebabkan karena tekanan mekanikI. Traksi detachment
Pada saat proses pengaktifan kelas, sistem akan memanggil komponen web service untuk mendapatkan list schedule pengajar kemudian komponen web service akan
Rendahnya nilai hasil belajar Ilmu Pengetahuan Alam siswa kelas 1v di Sekolah Dasar Kecil (SDK) Padat Karya Kecamatan Bolano Lambunu menjadi latar belakang
Akan tetapi guru ataupun lembaga agama yang akan mcnggunakan musik n1syid sebagai mctodcnya harus memperhatikan terlebih dahulu latar belakang (kondisi
[r]
[r]
Some explanations supporting it shows that the post-school program will be directed to the competence effectively manage adulthood life in society with aspects of being: able