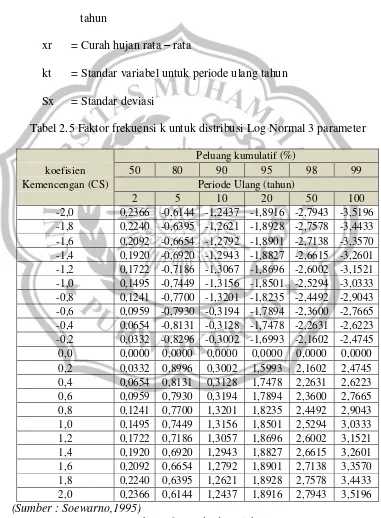
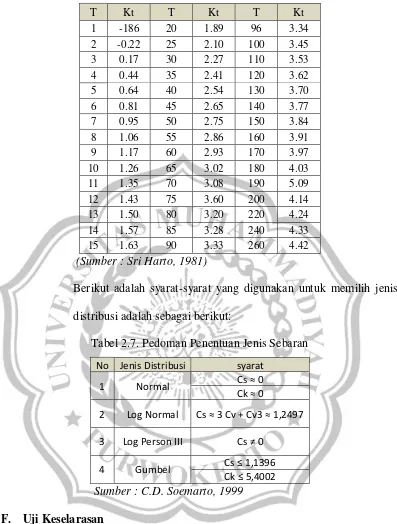
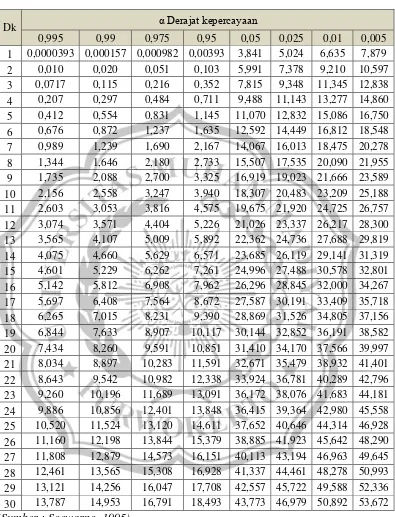
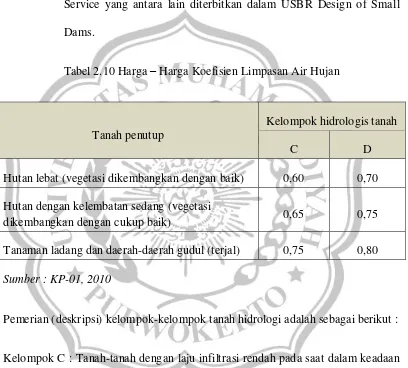
BAB II KAJIAN PUSTAKA A. Tinjauan Umum - WAHLUL SODIKIN BAB II
Teks penuh
Gambar




Dokumen terkait
Seperti halnya dengan parameter pertumbuhan tanaman, pengaruh aktifitas nitrat reduktase yang meningkat tetapi nitrogen yang tersedia terbatas menjadikan hasil dari
Menerapkan sebuah program gerakan literasi guna untuk meningkatkan minat baca kepada siswa dan perpustakaan menjadi salah satu fasilitas yang dapat digunakan
Pengenalan suara merupakan salah satu teknik dalam menerapkan sistem keamanan yang membutuhkan autentifikasi user, pengenalan suara telah menjadi bahan
Setelah dibuat adukan semen dan pasir (bahan plesteran) dengan perbandingan 1 semen : 2 pasir, maka dilakukan pemasangan batu bata untuk dinding saluran dan dasar saluran
1. partisipasi aktif dalam proyek perancangan yang berlangsung di PT. Envirospace Consultant Indonesia baik kegiatan di studio maupun di lapangan. Proyek perancangan vertical
Sedangkan pada Retribusi daerah dilaksanakan penyesuaian terutama pada Retribusi Layanan Kesehatan khususnya yang bersumber pada Jamkesmas (Jaminan Kesehatan Masyarakat)
Logika berasal dari kata Yunani kuno λόγος (logos) yang berarti hasil pertimbangan akal pikiran yang diutarakan lewat kata dan dinyatakan
Dalam dunia perbankan, yang dimaksud dengan konsep manajemen pemasaran adalah upaya untuk mencapai kepuasan nasabah terhadap penggunaan produk yang dikeluarkan oleh pihak bank,