Modul Matematika SMP kelas 9
Teks penuh
Gambar


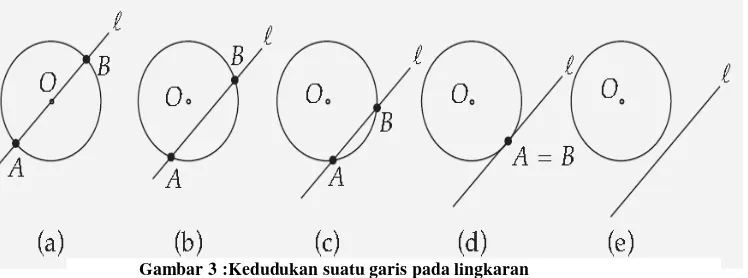
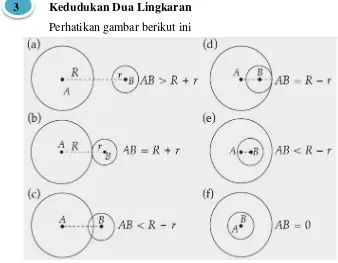
Garis besar
Dokumen terkait
Jarak dua titik pusat lingkran 26 cm,sedangkan panjang garis singgung persekutuan luarnya 24 cm, jika panjang jari – jari lingkaran yang satu adalah 15 cm, maka panjang jari –
.lika panjang garis singgung persekutuan luarnya 24 crn, maka jarak titik pusat kedua lingkaran adalah .... Banyaknya rusuk dan sisi limas
Panjang garis singgung persekutuan dalam antara lingkaran P dan Q dengan jari-jari secara berturut- turut 15 cm dan 17 cm serta jarak kedua titik pusat lingkaran 25 cm adalah …
Jika di ketahui jarak kedua lingkaran adalah 15 cm panjang jari – jari yang pertama adalah 6 cm dan jari – jari ke dua adalah 3 cm , maka tentukan panjang garis singgung
Jika jarak kedua pusat lingkaran 78 cm, maka panjang garis singgung persekutuan dalam kedua lingkaran adalah ….. Lingkaran yang melalui ketiga titik sudut suatu segitiga
Perhatikan gambar disamping, Diketahui empat lingkaran denganpusat P,Q,R dan S dan panjang masing-masing diameternya 14 cm , maka luas daerah yang diarsir adalah
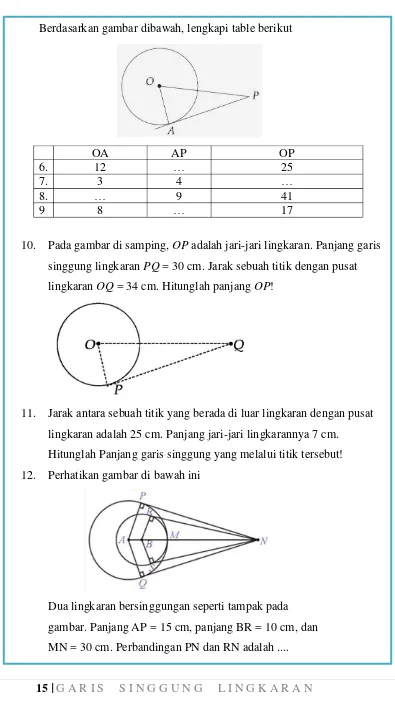
Pada gambar diatas, PQ adalah garis singgung persekutuan dalam dua lingkaran yang berpusat di A dan B..
Jika panjang garis persekutuan dalam kedua lingkaran tersebut adalah 8 cm maka jarak kedua titik pusat lingkaran tersebut adalah.... Dua buah lingkaran masing-masing berjari-jari 15 cm