Analisa Korelasi Terhadap Faktor Yang Mempengaruhi Ketersediaan Beras Di Kabupaten Tapanuli Utara.
Teks penuh
Gambar
Dokumen terkait
Nilai Adjusted R Square sebagai nilai yang disarankan dapat diketahui besarnya adalah 0,988 yang artinya variabel bebas harga beras impor ( ), jumlah produksi beras ( ), dan
Sedangkan pengujian secara parsial variabel Jumlah Penduduk (X 1 ) tidak berpengaruh secara nyata positif terhadap Permintaan Impor Beras Di Indonesia (Y).. Variabel Produksi Beras
Ada pengaruh harga domestik, harga impor, harga kedelai, luas panen jagung, konsumsi beras, dan jumlah tenaga kerja terhadap ketersediaan beras di Provinsi
Hasil pada model ketersediaan beras secara nasional dari tahun 1979-2008 menunjukkan bahwa dari enam variabel bebas (pengadaan dalam negeri, indeks nilai tukar
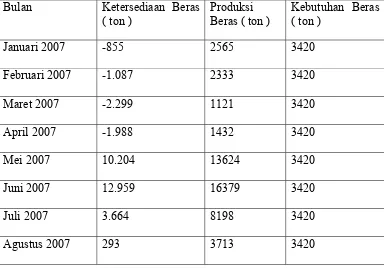
Penelitian ini mencoba untuk menguji bberapa faktor yang diduga memiliki pengaruh terhadap ketersediaan beras, yaitu produksi beras, kebutuhan beras, luas lahan dan jumlah
Ketersediaan beras di Sumatera Utara secara parsial dipengaruhi oleh harga beras domestik, harga kedelai domestik, konsumsi beras, dan jumlah tenaga kerja di
Hal ini menunjukkan bahwa H 0 diterima dan H 1 ditolak, yang berarti variabel bebas jumlah penduduk tidak berpengaruh nyata terhadap konsumsi beras Koefisien regresi X 1
Hasil Regresi Linear Berganda Menggunakan SPSS dengan Variabel Bebas, luas panen padi, harga beras, jumlah penduduk dan konsumsi beras di Sumatera Utara Tahun