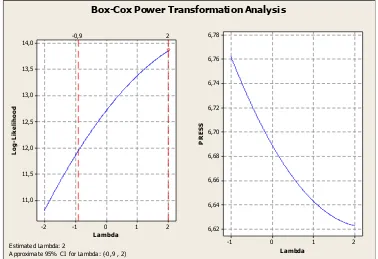
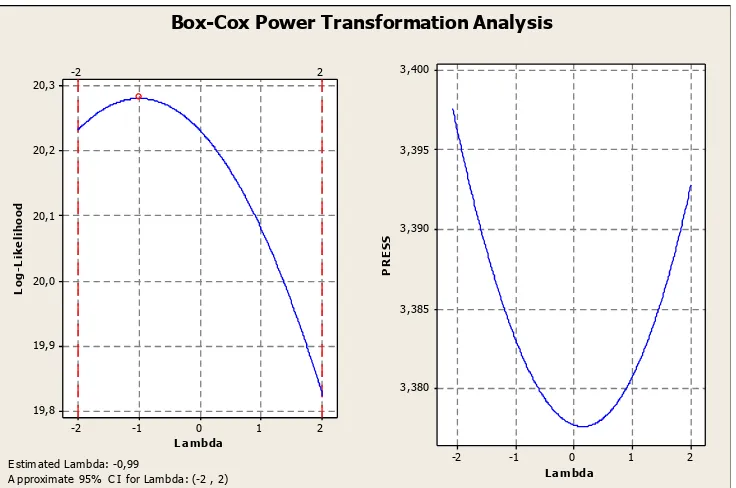
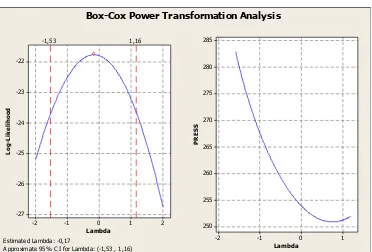
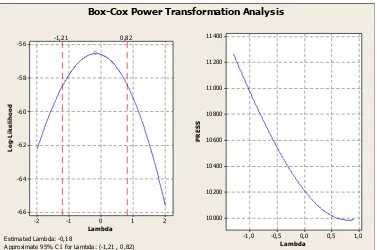
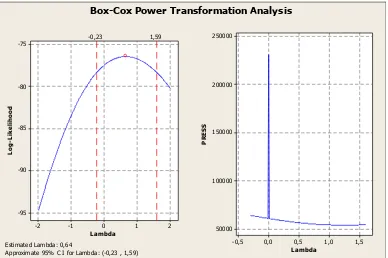
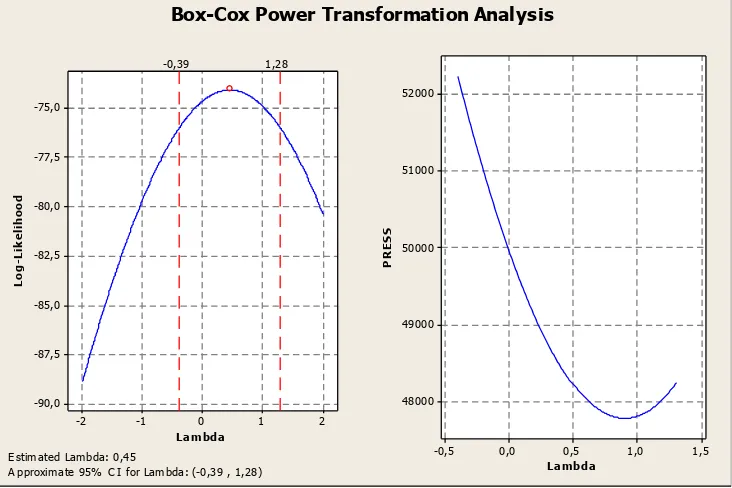
Analisis Transformasi Box Cox Untuk Mengatasi Heteroskedastisitas Dalam Model Regresi Linier Sederhana.
Teks penuh
Gambar
Dokumen terkait
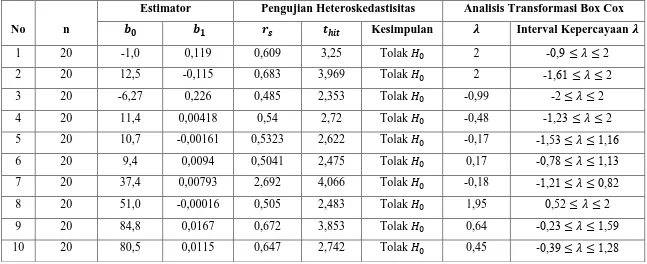
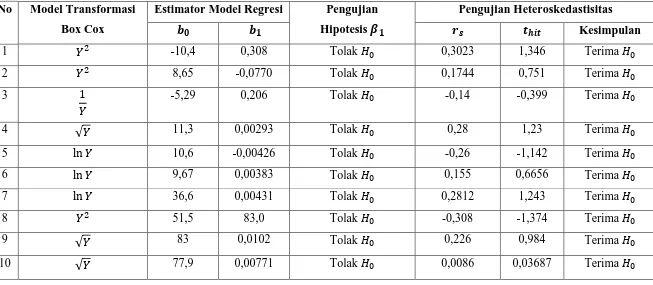
Dari hasil yang diperoleh diketahui bahwa penerapan transformasi Box-Cox pada OLS menghasilkan nilai � 2 lebih besar, nilai RMSE lebih kecil dan lebar selang
Dalam penulisan ini, penulis hanya akan membahas model regresi yang linier, dengan1. variabel terikat Y dengan variabel
Suatu model hubungan antara variabel prediktor X dan variabel respon Y, dalam hal ini adalah model regresi polinomial derajat 3 dengan heteroskedastisitas yang mempunyai
Metode statistika yang digunakan untuk membentuk model hubungan antara variabel terikat y dengan satu atau lebih variabel bebas x, di mana hubungan antara variabel tersebut linier
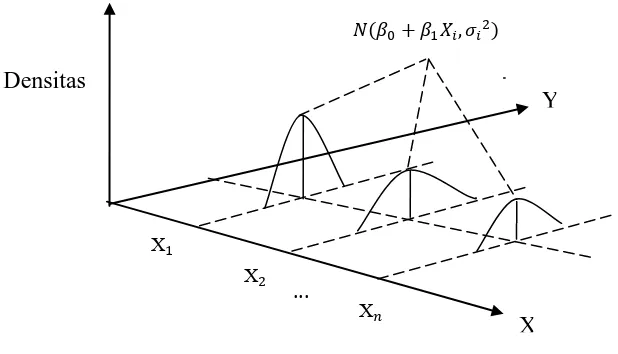
Dalam analisis regresi dikenal dua macam variabel at au peubah yait u variabel bebas X.. (independent variabel) adalah dan variabel t idak bebas Y (dependent
Analisis Regresi adalah metode statistika yang digunakan untuk menentukan kemungkinan bentuk hubungan / pengaruh antara dua atau lebih variabel bebas (X) dengan variabel terikat
Untuk mengakomodir konsep hubungan seperti di atas, dapat dilakukan analisis regresi linier ganda, yaitu dengan melibatkan variabel X lebih dari satu, dalam satu persamaan, dan
Regresi linier adalah metode statistika yang digunakan untuk membentuk model hubungan antara variabel terikat (dependen; respon; Y) dengan satu atau lebih variabel bebas