Kelas 10 SMA Matematika Siswa Semester 1
Teks penuh
Gambar
Dokumen terkait
Selain menggunakan diagram panah dan kartesius, sebuah relasi yang menghubungkan himpunan yang satu dengan himpunan lainnya dapat disajikan dalam bentuk himpunan pasangan
Jika kita mengetahui persamaan lengkungan tersebut, kita akan dapat dengan mudah menentukan luas daerah yang dibatasi oleh kurva itu dan badan jalan bahkan kita juga dapat
1) Relasi dapat terbentuk apabila terdapat dua buah atau lebih himpunan/kelompok yang memiliki anggota yang akan dipasangkan satu dengan yang lain. Pada Gambar 5.1, himpunan
Jika semua himpunan di bawah pertimbangan adalah himpunan bagian dari suatu himpunan S tertentu, maka himpunan S disebut himpunan
Jika mobil tersebut sampai di tujuannya dalam waktu 2 jam, berapakah jarak yang telah ditempuh oleh mobil tersebut sampai ke tujuan.. Isilah titik-titik di bawah ini
1) Relasi dapat terbentuk apabila terdapat dua buah atau lebih himpunan/kelompok yang memiliki anggota yang akan dipasangkan satu dengan yang lain. Pada Gambar 5.1, himpunan
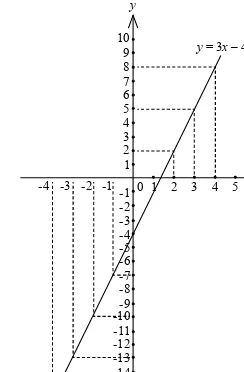
Jawaban: Langkah 1: Menentukan persamaan grafik Persamaan grafik yang memotong sumbu X di titik –4, 0 dan –1, 0: Kembali ke daftar isi Kembali ke awal bab... Persamaan grafik yang
Peluang suatu kejadian • Percobaan: percobaan adalah suatu tindakan atau kegiatan yang dapat memberikan beberapa kemungkinan hasil • Ruang Sampel: ruang sampel adalah himpunan