Model optimasi pendistribusian logistik bencana alam
Teks penuh
Gambar


Dokumen terkait
“Sistem Informasi Manajemen Penanggulangan Bencana“ ini diharapkan dapat membantu tim evakuasi dalam proses menolong korban bencana alam melalui data permintaan bantuan,
Dari penelitian ini dihasilkan sebuah sistem informasi manajemen bantuan logistik pasca bencana alam berbasis mobile web yang dapat memberikan informasi kepada
Badan Kesbanglinmas PB, yang terkena dampak pada saat melakukan tugas dalam penanganan bencana alam diwilayah Kabupaten sleman. Ko6an bencana alam yang mengalami kerusakan
Maka dari itu penelitian yang akan dilakukan yaitu menentukan prioritas penerima bantuan akibat bencana alam dengan metode K-means Clustering, metode ini sering digunakan
(d) on update cascade delete no action, untuk menentukan aksi apa yang akan dilakukan pada sebuah baris dalam suatu tabel, pada penelitian ini salah satu tabel yang
Dari penelitian ini dihasilkan sebuah sistem informasi manajemen bantuan logistik pasca bencana alam berbasis mobile web yang dapat memberikan informasi kepada
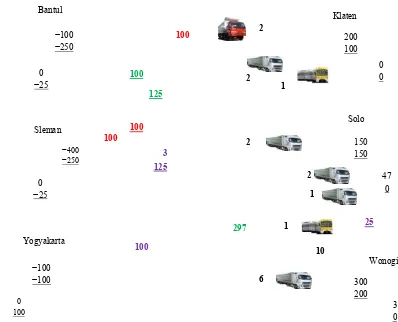
Berdasarkan tabel di atas, karena banyaknya garis tidak sama dengan banyaknya baris/kolom maka solusi belum optimal, sehingga angka yang tidak terkena garis harus
Web ini digunakan untuk mencari informasi tetntang bencana alam yang terjadi pada setiap daerah yang terkena bencana dapat mencari lebih detail mengenai korban, logistik, posko dan