MODEL VERHULST PADA PERTUMBUHAN POPULASI IKAN LELE TERNAK
Teks penuh
Gambar
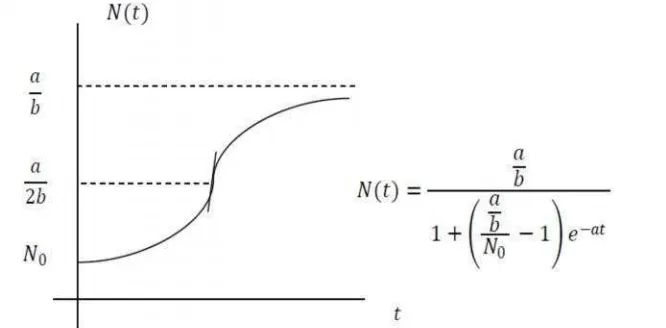
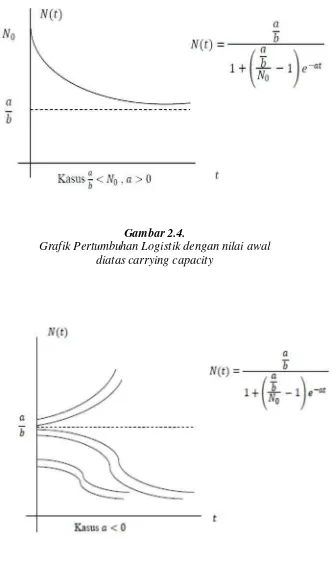
Dokumen terkait
Tujuan penelitian ini untuk mengetahui pengaruh frekuensi pemberian pakan terhadap laju pertumbuhan pada pendederan ikan lele Sangkuriang Clarias sp.. Pengaturan frekuensi
Skripsi saya yang berjudu l “Strategi Pengembangan Bisnis Pada Peternakan Bibit Ikan Lele di Kota Binjai (Studi Kasus Pada Ternak Lele Asio Jalan Lincun Binjai Barat)”, sebagai
Menyatakan bahwa skripsi yang berjudul “ Pengaruh Pemberian Enzim Papain Pada Pakan Terhadap Kelangsungan Hidup dan Laju Pertumbuhan Benih Ikan Lele Dumbo (Clarias
Berdasarkan hasil percobaan mengenai pengaruh populasi lele dan jenis media tanam terhadap pertumbuhan dan hasil tanaman bayam yang ditanama pada sistem akuaponik
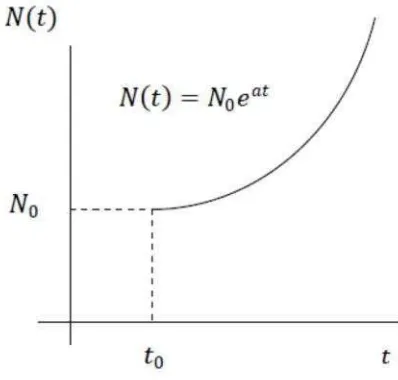
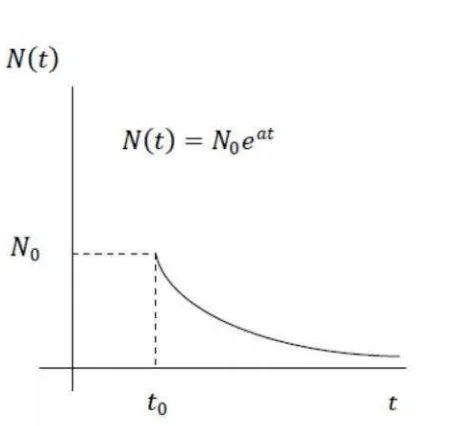
Oleh karena itu, pada kesempatan kali ini penulis akan mencoba mengaitkan antara laju pertumbuhan populasi dari model pertumbuhan populasi logistik dengan epidemi
Meskipun heritabilitas karakter pertumbuhan pada pembentukan populasi generasi pertama ikan lele Afrika tumbuh cepat melalui seleksi individu ini tergolong rendah, tetapi
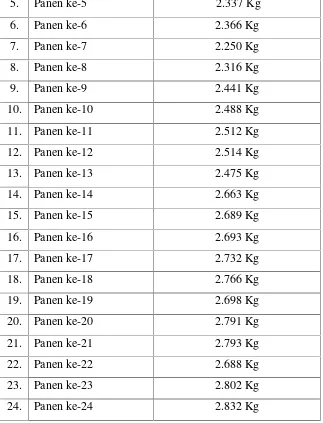
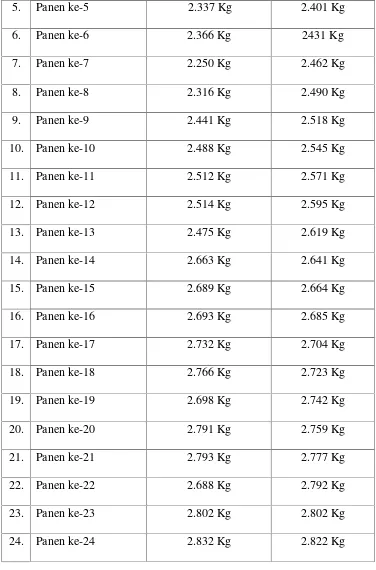
Pertumbuhan ikan lele pada umur 30 hari dengan rata-rata pertumbuhan Ikan Lele adalah 3,05, sementara pada kolam kedua rata-rata pertumbuhan ikan Lele adalah 4,75,
Hasil penelitian menunjukkan bahwa nilai efisiensi pakan terbaik pada pakan kontrol (pelet) sebesar 77,61%, laju pertumbuhan harian ikan lele sangkuriang yang terbaik