PENGARUH MODEL PROBLEM BASED LEARNING TERHADAP KEMAMPUAN PEMECAHAN MASALAH MATEMATIS SISWA
Teks penuh
Gambar
Dokumen terkait
Motor tetap (Fixed) dengan ekor terikat pada satu struktur sitoskeleton ketika motor berinteraksi dengan sitoskeleton lain struktur sitoskeleton meluncur. MOTOR TETAP (Motor
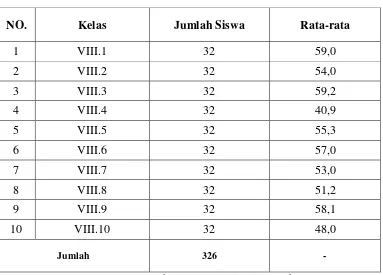
Hal-hal yang menyebabkan kemampuan pemecahan masalah matematis siswa yang mengikuti model PBL lebih tinggi dibanding- kan siswa yang mengikuti pem- belajaran
Berdasarkan hasil penelitian diketahui temperatur maksimum sebesar 58,4 o C, nilai maksimum dari rata–rata efisiensi kolektor sebesar 0,825 %, dan efisiensi sistem sebesar 35,907
produksi dan rencana target produksi dari alat tersebut. Kebutuhan alat angkut dan alat muat setiap tahun cenderungan meningkat, hal ini disebapkan oleh target produksi
PENENTUAN KADAR PROTEIN PADA TAUCO DENGAN METODE KJELDAHL DIBALAI BESAR PENGAWAS OBAT DAN MAKANAN MEDAN..
w imr Kecepatan angin induksi arah vertikal pada rotor utama m/s. w hf Kecepatan angin relatif arah vertikal, lokal di sirip horisontal
RINCIAN DOKUMEN PELAKSANAAN PERUBAHAN ANGGARAN BELANJA TIDAK LANGSUNG SATUAN KERJA PERANGKAT DAERAH. BERTAMBAH/
Berdasarkan hasil analisis sidik ragam varian (ANOVA) menunjukan bahwa pada permen jelly dengan perlakuan konsentrasi rumput laut menunjukan adanya pengaruh yang nyata