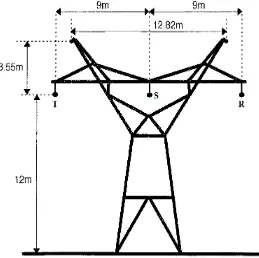
Pengaruh Konfigurasi Kawat Penghantar Saluran Transmisi Sirkuit Ganda (Double Circuit ) Terhadap Kuat Medan Listrik Di Bawah Saluran Transmisi.
Teks penuh
Gambar
Dokumen terkait
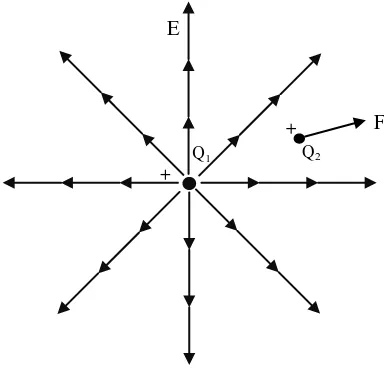
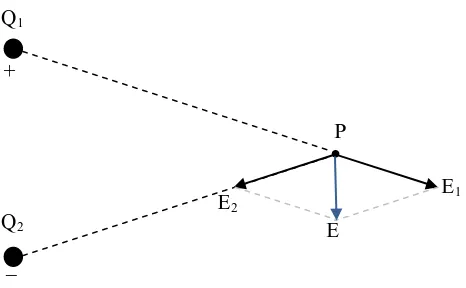
• Dari hasil perhitungan diperoleh bahwa: untuk ketinggian titik uji ≤ 18m, kuat medan listrik maksimum diperoleh di sumbu menara (titik nol).
Untuk itu pada tugas akhir ini dilakukan studi perbandingan terhadap induktansi saluran, kapasitansi saluran, serta kuat medan lisrik yang timbul di bawah saluran
Untuk itu pada tugas akhir ini dilakukan studi perbandingan terhadap induktansi saluran, kapasitansi saluran, serta kuat medan lisrik yang timbul di bawah saluran
Untuk itu pada tugas akhir ini dilakukan studi perbandingan terhadap induktansi saluran, kapasitansi saluran, serta kuat medan lisrik yang timbul di bawah saluran
Pengaruh Konfigurasi Kawat Penghantar Saluran Transmisi Sirkuit Ganda Terhadap Kuat Medan Listrik Di Bawah Saluran Transmisi.. Tugas Akhir Teknik
Dengan penggunaan alat ukur tegangan dan arus induksi dapat diberikan suatu persamaan empiris yang dapat digunakan untuk menghitung kuat medan listrik dan
Perhitungan Kuat Medan Listrik Di Bawah Saluran Transmisi Studi Kasus : Perencanaan Transmisi 27 5 kV Galang-Binjai Studi Pengaruh Korona Terhadap Surja Tegangan Lebih Pada Saluran