• Tidak ada hasil yang ditemukan

abstraction processes in learning geomet

N/A
N/A
Info
Unduh - Bebas
Protected

Academic year: 2017

Membagikan "abstraction processes in learning geomet"

Copied!
9
0
0

Memuat.... (Lihat teks lengkap sekarang)

Unduh sekarang ( 9 Halaman )

Teks penuh

Loading

Gambar

Table 1:The Relationships between van Hiele’s Model of Teaching Geometry and the Aspects of Abstraction Process
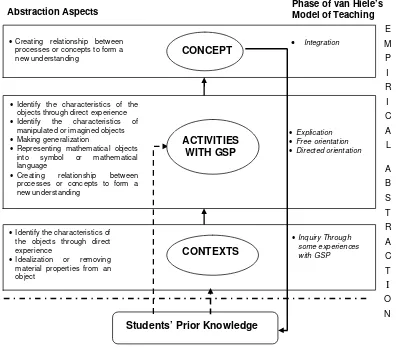
Figure 1. Flowchart of Students’ Abstraction Process in Learning Triangle Using GSP

Referensi

Unduh sekarang ( PDF - 9 Halaman - 117.17 KB )

Garis besar

abstraction processes in learning geomet

Dokumen terkait

Pembelajaran Menyenangkan dengan Seni Te

Tujuan penelitian ini adalah (1) mendeskripsikan pelaksanaan pembelajaran menyenangkan dengan buku seni budaya tematik berbasis keMIPA-an untuk SD, (2) mendeskripsikan

KAJIAN TEKNIS DAN EKONOMIS PEMANFAATAN LIMBAH BATU BARA (FLY ASH) PADA PRODUKSI PAVING BLOCK.

[r]

PANDANGAN STAKEHOLDERS PENDIDIKAN SUKU BATAK TOBA TENTANG PENDIDIKAN ANAK PENYANDANG DISABILITAS DAN IMPLEMENTASINYA DI KABUPATEN TOBA SAMOSIR.

Para Stakeholders pendidikan mengetahui dengan baik pandangan- pandangan dalam masyarakat suku Batak Toba tentang anak penyandang disabilitas dan dampak-dampak yang

PENDAHULUAN Meningkatkan Kecerdasan Linguistik Melalui Cerita Bergambar Pada Anak TK Kelompok B TK ‘Aisyiyah II Babadan, Karangdowo Tahun Pelajaran 2011/2012.

Hal ini dapat merangsang berkembangnya komponen kecerdasan linguistik yang paling penting, yaitu kemampuan menggunakan bahasa untuk mencapai sasaran praktis sesuai

PERSEPSI NASABAH TERHADAP SISTEM E-COMMERCE PADA BNI LIFE SYARIAH KANTOR CABANG YOGYAKARTA

[r]

Institutional Repository | Satya Wacana Christian University: Identifikasi Hasil Belajar Matematika Siswa Kelas V SD Negeri Kesongo 01 Tuntang Ditinjau dari Dukungan Sosial Orang Tua T1 202009063 BAB I

Hal ini, orang tua harus berperan aktif dalam mendidik anak belajar di rumah untuk menjadikan berprestasi di sekolah, mulai dari mangatur kegiatan anak sehari-hari,

Penyelesaian Sengketa Pembebasan Tanah Ulayat untuk Pembangunan Bandar Udara Silambo Kabupaten Nias Selatan Provinsi Sumatera Utara

Dalam melaksanakan wewenang pengaturan tersebut, hal yang sudah disadari oleh pembentuk UUPA, bahwa hukum tanah yang dibangun itu harus didasarkan pada nilai-nilai

GAMBARAN KUALITAS HIDUP WANITA LANJUT USIA YANG MENGIKUTI SENAM GERAK LATIH OTAK DI PANTI SOSIAL TRESNA WREDHA BUDI PERTIWI BANDUNG.

GAMBARAN KUALITAS HIDUP PADA WANITA LANJUT USIA YANG MENGIKUTI SENAM GERAK LATIH OTAK.. DI PANTI TRESNA WREDHA BUDI

Image