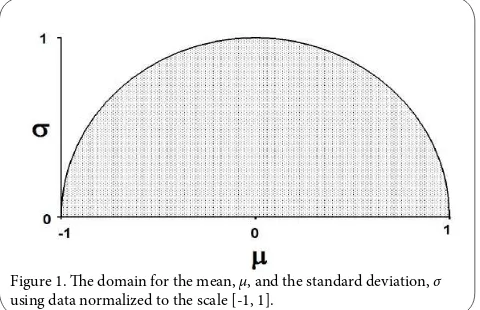
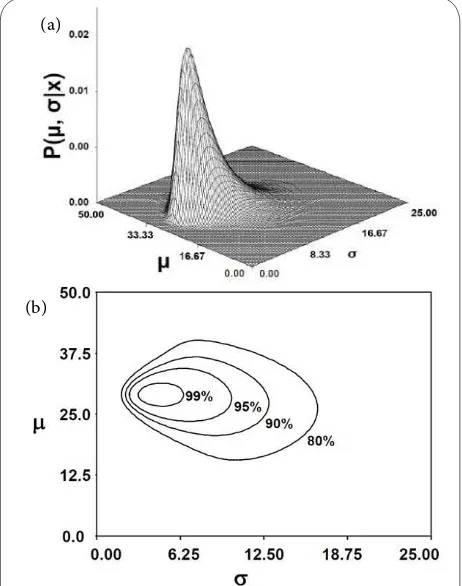
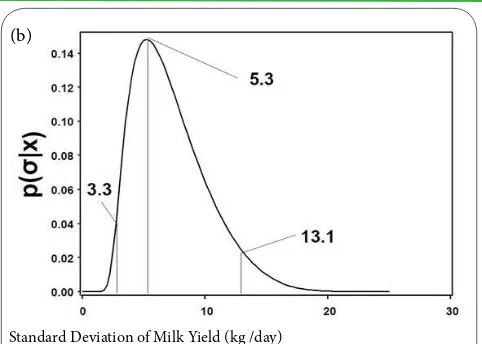
Probability Distributions for the Mean a
Teks penuh
Gambar
Dokumen terkait
[r]
[r]
Oleh itu, beberapa cadangan penambahbaikan telah disyorkan, seperti mengamalkan sikap autokratik pada sesetengah situasi, mengaplikasikan Teori Pertukaran Pemimpin Ahli dan
Demikian Berita Acara Pembukaan Penawaran ( BAPP ) ini dibuat dengan sebenarnya, ditandatangani bersama oleh Panitia Pokja VI Unit Layanan Pengadaan ( ULP ) Kota Banjarbaru ,
Tempat : Kantor Dinas Pertambangan dan Energi Kabupaten Pelalawan Adapun daftar peserta yang dinyatakan Lulus mengikuti pembuktian kualifikasi sebagai berikut :.. No Nama
Kelengkapan yang harus dibawa pada saat Pembuktian Kualifikasi adalah ”BERKAS ASLI” file Dokumen Penawaran (Dokumen Penawaran Harga, Administrasi dan Teknis) serta Dokumen
[r]
dengan suatu erupsi gigi permanen ataupun erupsi gigi desidui. Kista erupsi memperlihatkan suatu pembengkakan yang halus menutupi gigi yang erupsi, dengan warna berbeda dari