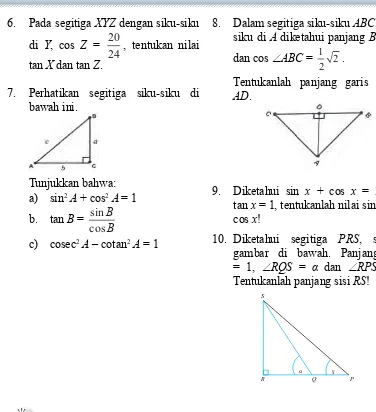
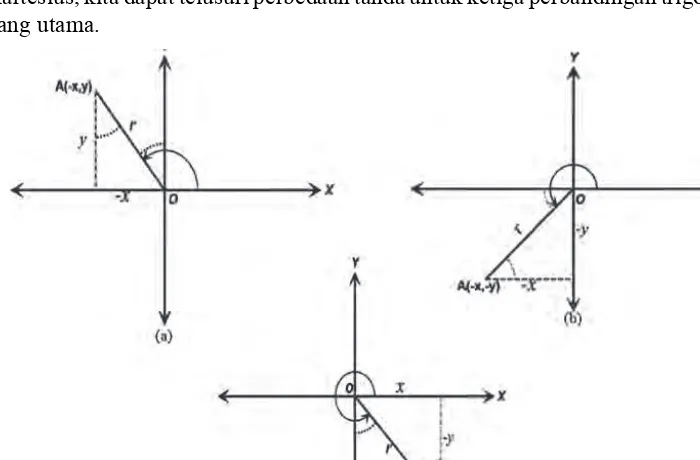
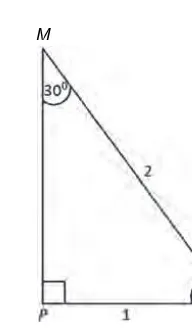
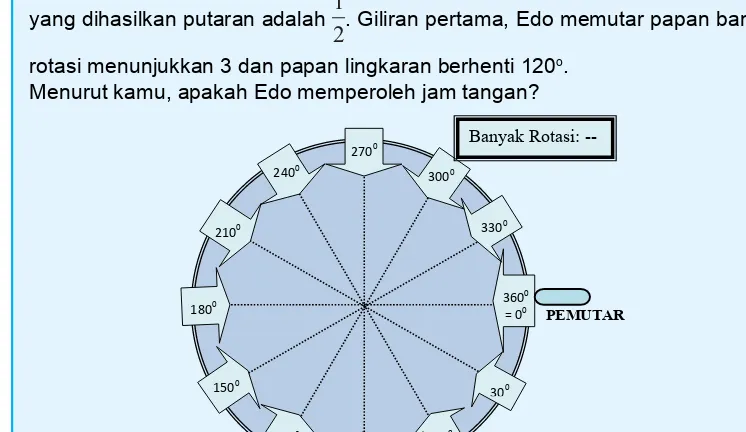
Kelas 10 SMA Matematika Siswa Semester 2
Teks penuh
Gambar


Dokumen terkait
pemilik toko tersebut, maka jumlah pelangganmu yang akan mendapat bagian setoran kain adalah .... Dari gambar di atas bangun yang sebangun adalah
Setelah membahas materi persamaan dan pertidaksamaan linear satu variabel yang melibatkan konsep nilai mutlak, maka dapat diambil berbagai kesimpulan sebagai acuan untuk
yang menempati tempat saruan pada bilangan 375 adalah angka.. kelereng ardo 98 kemudian membeli lagi 89 kelereng
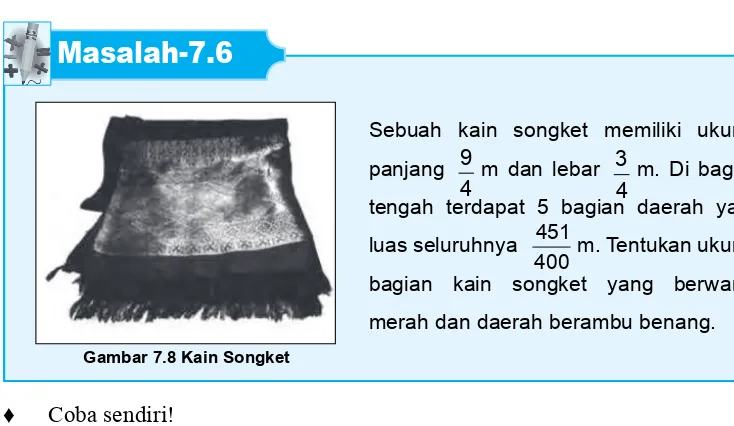
Merupakan contoh songket Balapak yang di hiasi hampir semua bagian kain dengan benang logam, motifnyapun terdiri dari beberapa motif khas Sumatera Barat, seperti:
Apabila pada bagian pernyataan umum terdapat kalimat definisi dan kalimat pengklasifikasian, dalam bagian deskripsi bagian kamu akan menemukan kalimat deskripsi. Perhatikan
Berilah contoh lain mengenai pengaruh kebudayaan lokal pada kebudayaan nasional1. Berilah contoh lain mengenai pengaruh kebudayaan nasional pada
Perhatikan bahwa bola yang berasal dari gelas B tidak boleh diambil pada pengambilan ketujuh.. Proses pengambilan bola dilakukan tepat
@2020, Direktorat SMA, Direktorat Jenderal PAUD, DIKDAS dan DIKMEN 8 Contoh lain misalkan, seseorang yang akan membuat suatu area penempatan hewan peliharaan kuda, kambing, atau ayam