ANALISIS KEMAMPUAN SISWA SMP DALAM MENYELESAIKAN SOAL PISA KONTEN SHAPE AND SPACE BERDASARKAN MODEL RASCH
Teks penuh
Gambar
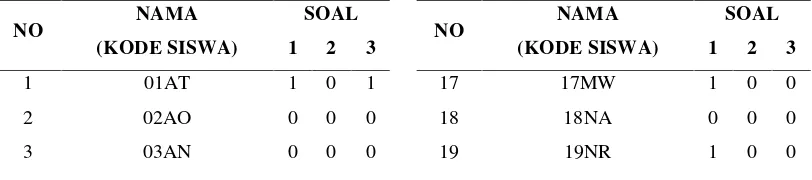
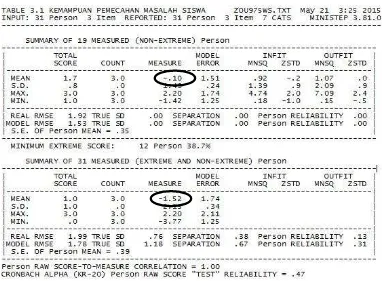

Dokumen terkait
12 Tahun 2014 tentang persyaratan mutu obat tradisional memberi batasan jamu gendong adalah jamu yang diracik, dicampur, diolah, dan diedarkan sebagai obat
Beberapa perbedaan pendapat yang ada berkembang pada kebebasan berpindah agama yang tidak dapat diterima oleh partai-partai islam, masalah-masalah yang berkaitan
Seluruh anggota Gerwani saat itu ikut diburu karena organisasi mereka dekat dengan PKI. Sejumlah pejabat tinggi Gerwani pun merangkap anggota PKI. Maka ketika PKI disebut
Antusias peserta coaching clinic sepak bola SSB Tunas Kaili dan SSB Rauf Junior merupakan modal dalam melakukan kegiatan ini, dengan tidak melakukan penjelasan
Puji syukur yang teramat dalam saya haturkan ke hadirat Tuhan Yang Maha Segala, atas percikan kasih, hidayat, dan aifiq-Nya sehingga Skripsi dengan judul „Analisis
a. Agar sekolah memberikan pencerahan kepada siswa/i pentingnya pemeriksaan golongan darah pada setiap anak didik. Bagi dosenSTIKes Prima Nusantara Bukittinggi, program
Lamanya waktu perendaman semaian karet GT1 pada media tanam yang ditambahkan larutan osmotikum PEG 6000 menunjukkan pengaruh yang berbeda nyata terhadap
Pada prinsipnya Pendidikan Agama Islam adalah proses pembentukan kepribadian individu sesuai dengan nilai-nilai ilahiyah, sehingga individu yang bersangkutan dapat