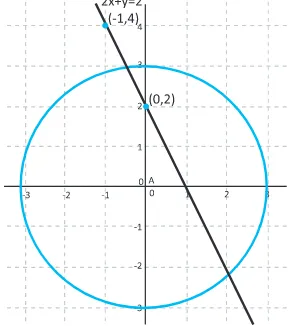
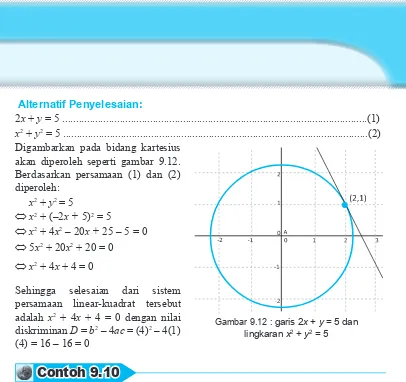
Buku pegangan siswa matematika sma kelas
Teks penuh
Gambar
Dokumen terkait
Menganalisis fungsi sosial, struktur teks, dan unsur kebahasaan dari teks news item berbentuk berita sederhana dari koran/radio/TV, sesuai dengan konteks penggunaannya..
Menganalisis fungsi sosial, struktur teks, dan unsur kebahasaan dari teks news item berbentuk berita sederhana dari koran/radio/TV, sesuai dengan konteks penggunaannya..
4.32.3 Menyelesaiakn masalah kontekstual yang berkaitan dengan nilai, titik, jenis stasioner dan nilai maksimum dan minimum turunan fungsi aljabar Jurnal Kuis (Soal Pilihan
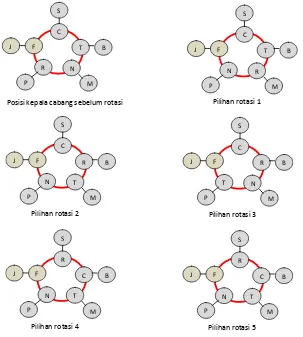
Yang akan kita bicarakan hanya titik –titik puncak (stasioner), belok datar dan belok miring (disebut titik belok karena arah berubah grafik fungsi turunan pertama mencapai
Berdasarkan gra…k fungsi f berikut, tentukanlah: i) titik ujung, ii) titik stasioner, iii) titik singular, iv) nilai maksimum/minimum mutlak, v) nilai maksimum/minimum
Jika salah satu bilangan kita sebut (positif) maka bilangan yang lain adalah ( + 20).. Kurva fungsi dalam contoh ini terlihat pada Gb.9.9.. Jika turunan pertama fungsi ini
| www.pakical.xyz 3.31 Menentukan turunan fungsi aljabar menggunakan definisi limit fungsi atau sifat-sifat turunan fungsi serta penerapannya 3.32 Menganalisis keberkaitan turunan
Ayo Berdiskusi Eksplorasi 6.4 Menyelidiki peran nilai c dalam grafik fungsi kuadrat Untuk setiap grafik fungsi yang telah kalian buat, tentukan koordinat titik potong grafik dengan