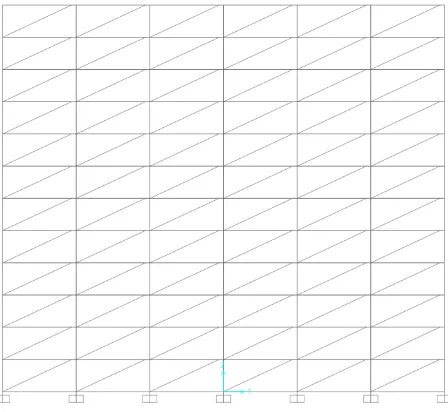
Evaluasi Kinerja Struktur Bangunan Baja dengan Menggunakan Pengaku Eksentris (EBF)
Teks penuh
Gambar

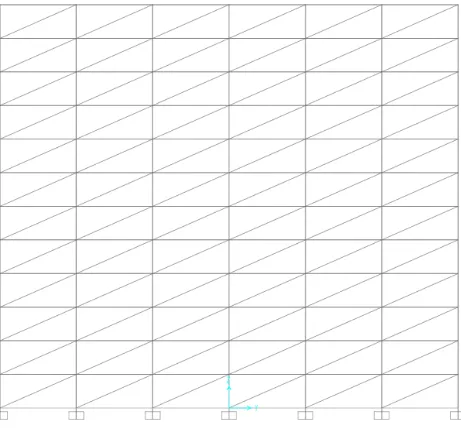

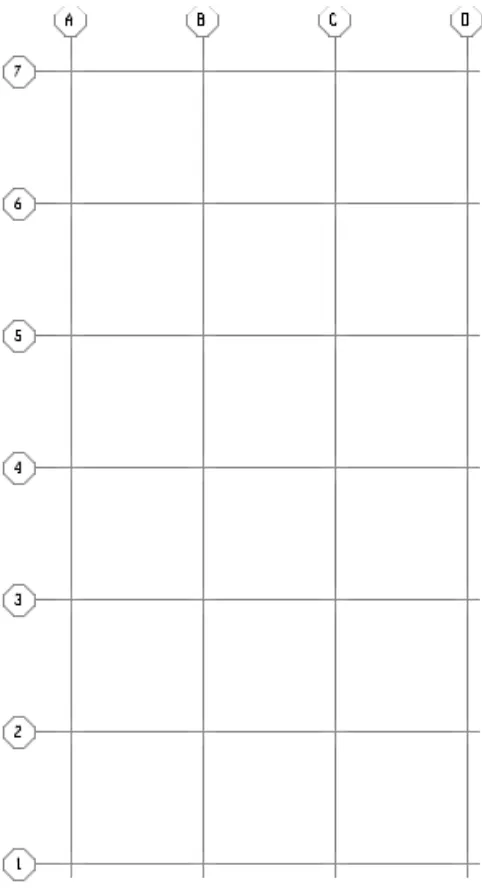
Dokumen terkait
Nilai penjualan besi baja digunakan untuk menghitung CR4 karena terkait dengan kemampuan perusahaan-perusahaan untuk bersaing dalam produk besi baja, sehingga yang dilihat
kenampakan pada citra satelit berwarna hijau dengan tingkat kecerahan gelap sampai sangat gelap untuk tanaman tua, dan terang untuk tanaman muda, tekstur kasar untuk tanaman tua
Pada tahun 1991, ikan- ikan yang berumur 2 tahun (kelas umur 1989) dan 3 tahun (kelas umur 1988) hanya 4% dari total tangkapan, sedangkan sisanya adalah ikan-ikan dengan komposisi
Angka tersebut dapat turun dengan pemberian profilaksis vitamin K pada bayi baru lahir.... Akibat PDVK adalah terjadinya perdarahan otak dengan angka kematian
• Sementara menurut U.S Departement of Health, Education and Wolfare memberikan definisi Child abuse sebagai kekerasan fisik atau mental, kekerasan seksual dan penelantaran terhadap
Berdasarkan hasil analisis dapat diketahui bahwa ada pengaruh pijat bayi terhadap perubahan berat badan pada bayi usia 6 -12 bulan di Wilayah Kerja Puskesmas
Wakaf am ialah harta pemberian selama-lamanya dan segala pendapatan daripada harta itu turun-temurun bagi penggunaan agam Islam atau faedah umum yang diharuskan oleh agama Islam
Berdasarkan dari jawaban siswa pada Gambar 3, terlihat bahwa siswa tidak mampu menjawab. Sehingga pada soal nomor 3, kemampuan pemahaman matematik siswa