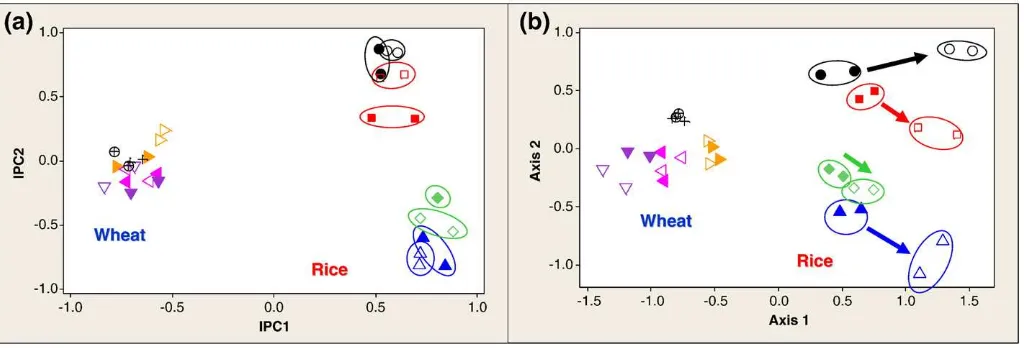
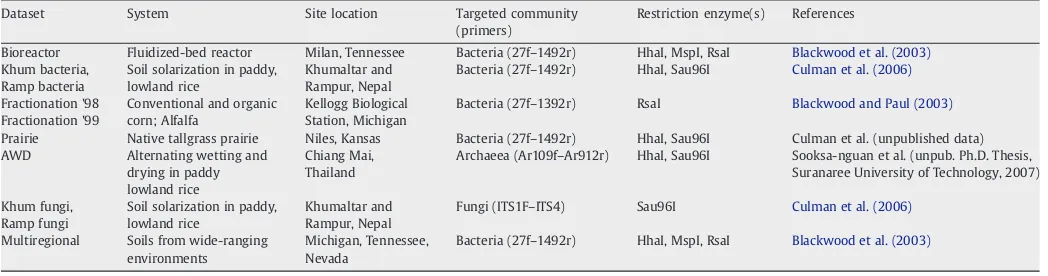
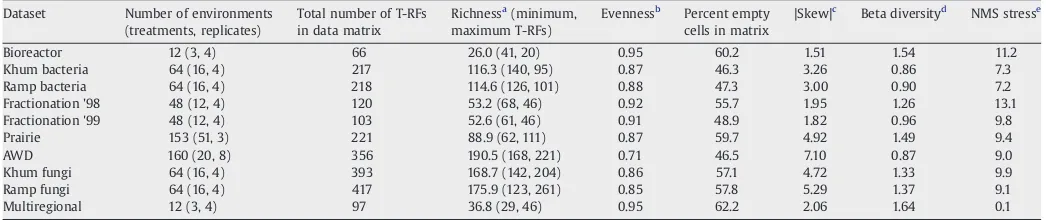
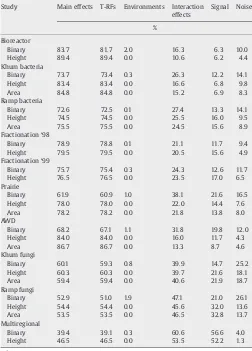
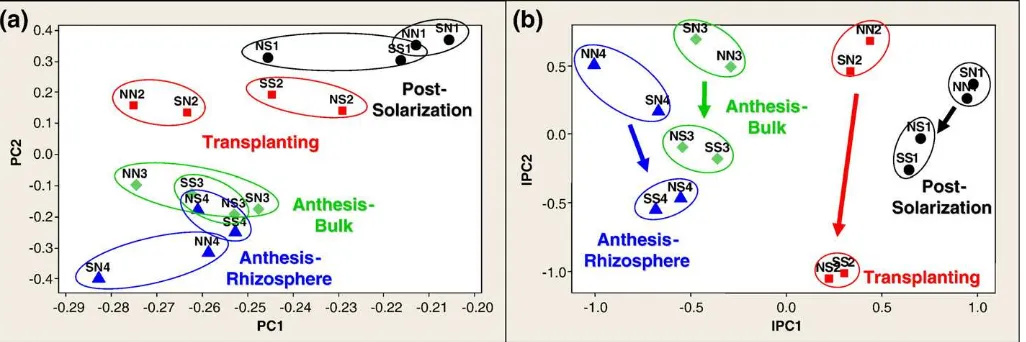
Analysis of T RFLP data using analysis o
Teks penuh
Gambar
Garis besar
Dokumen terkait
Berdasarkan hasil perhitungan yang telah dilakukan, data kemudian diolah dengan menggunakan software Res2dinv sehingga didapatkan hasil gambar kontur lapisan bawah
membuat dan memberikan faktur/nota pembelian beserta obat-obat yang dipesan kepada bagian pembelian. 4) Bagian gudang akan memeriksa obat yang masuk sesuai dengan SPO
Tujuan utama dari layanan Bimbingan dan Konseling (BK) di sekolah adalah untuk membantu agar peserta didik dapat : (1) merencanakan kegiatan penyelesaian studi, perkembangan karir
Penelitian ini bertujuan untuk mengetahui tingkah laku menyusu, makan dan pertambahan bobot badan (PBB) cempe pada jenis kelamin jantan dan betina berumur kurang
akan menciptakan value added bagi perusahaan sehingga dapat berpengaruh terhadap kinerja keuangan perusahaan, pertumbuhan perusahaan, dan nilai pasar.. Penciptaan value added
Program studi Akuntansi Fakultas Ekonomi Universitas Kristen Krida Wacana sendiri tahun 2004 memperoleh peringkat akreditasi “C” dengan nilai 273 mengalami penurunan dari
Berdasarkan latar belakang diatas maka tujuan penelitian ini adalah untuk mengetahui bagaimana pengaruh suku bunga kredit modal kerja, non performing loan, pertumbuhan
Rifampisin diabsorbsi dengan baik melalui sistem gastrointestinal pada saat perut kosong (satu jam sebelum makan).. Anak dengan BB 15-19 kg dapat diberikan 3 tablet. Anak dengan