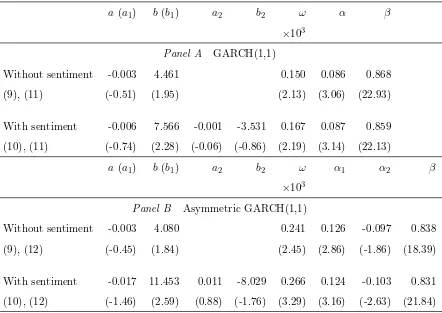
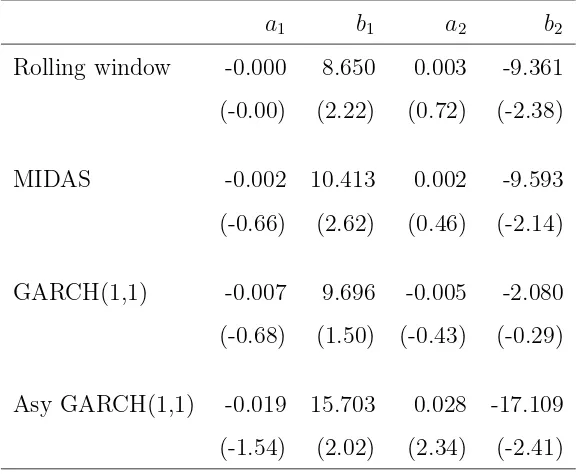
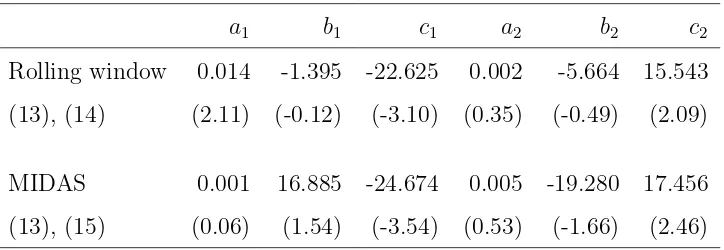
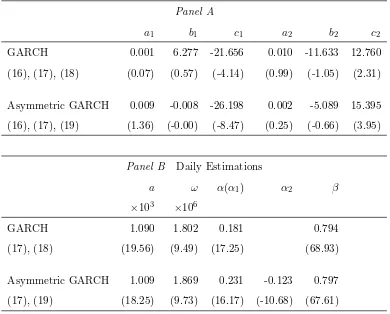
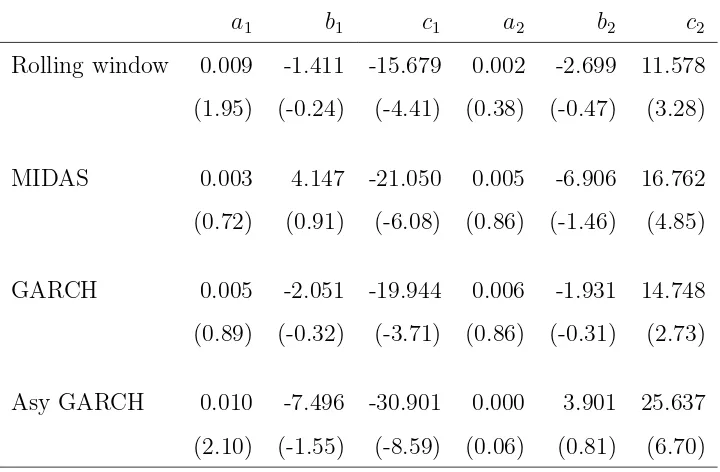
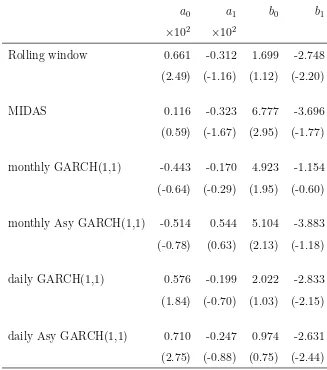
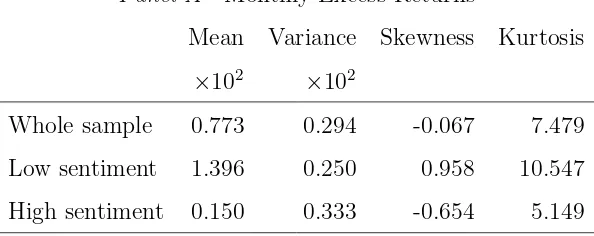
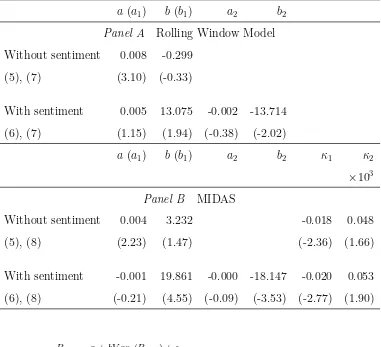
Investor sentiment and the mean variance
Teks penuh
Gambar
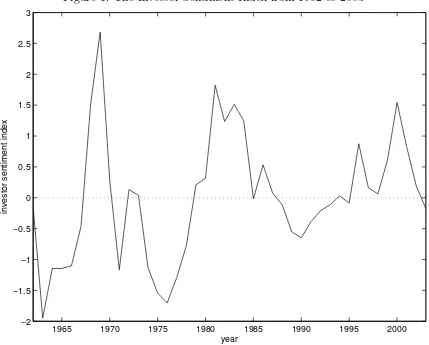
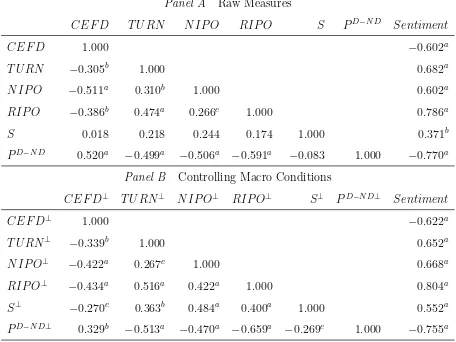
Garis besar
Dokumen terkait
For example, education about dual use issues could be incorporated into the channels through which life scientists already receive exposure to issues of responsible conduct,
- Otonomi Daerah, Pemerintahan Umum dan Administrasi Keuangan Urusan Pemerintahan. SATUAN KERJA
[r]
Laporan keuangan pada dasarnya adalah hasil dari proses akuntansi yang dapat digunakan sebagai alat untuk berkomunikasi antara data keuangan atau aktivitas suatu
[r]
Dengan menggunakan web saja pengguna dapat melihat daftar kegiatan yang ada di Universitas Kristen Petra, tidak hanya kegiatan yang sedang berlangsung saat ini ataupun yang
http://lpse.bekasikota.go.id oleh para Peserta Lelang dengan Panitia Pengadaan Barang/Jasa Badan Pengelolaan Keuangan dan Aset Daerah Kota Bekasi, dimulai Jam 13.00
Dari hasil penelitian menunjukkan bahwa hasil dari rep-PCR membentuk 5 kelompok bakteri, maka dari kelompok tersebut di ambil isolate yang mewakili kelompok