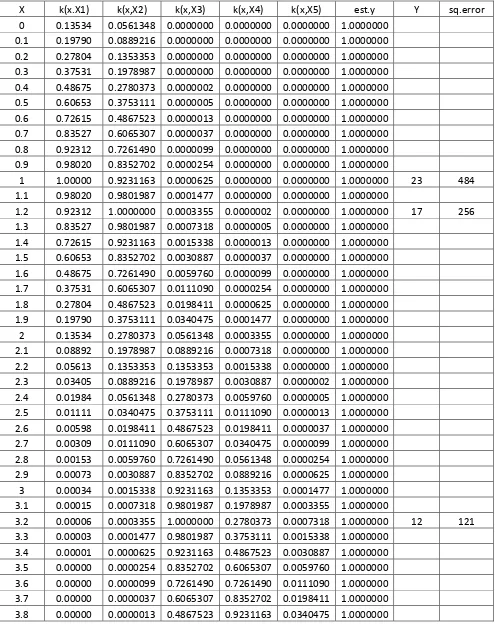
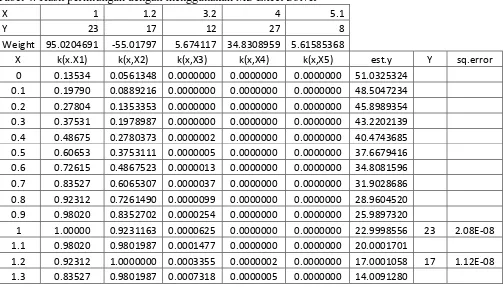
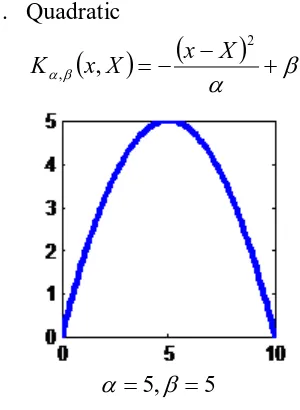
Fungsi Kernel Pada Metode Regresi Non-Parametrik
Teks penuh
Gambar

Garis besar
Dokumen terkait
Pada periode 2006-2007, kelompok sektor utilitas mendominasi PDRB Kabupaten Kepulauan Meranti, ini ditunjukkan oleh sumbangnnya yang menunjukkan angka paling besar terhadap
Produksi terjadi karena kerja sama empat faktor produksi, yaitu faktor produksi alam, tenaga kerja, modal dan pengusaha. Pengusaha ini yang mengkombinasikan faktor produksi
termasuk episode sporadik, episode sporadik yang didapat dari komunitas, dalam hal ini sistitis akut dan pielonefritis akut pada individu yang sehat.. • ISK ini banyak didapat
Berkaitan dengan target capaian pelaksanaan PKM ini, maka revitalisasi pemahaman paham Islam Ahlussunnah wal Jama’ah dan pengenalan diri pada Majelis Taklim Ummahat DDI
Fungsi Pelaksana sebagaimana dimaksud dalam Pasal 8 merupakan fungsi Pelaksana BPBD dilaksanakan secara terkoordinasi dan terintegrasi dengan satuan kerja perangkat
Jika tanah tidak mampu menahan air hujan di daerah yang tinggi maka akan terjadi.. Yang bukan merupakan upaya untuk mencegah tanah
khulu’ atau dengan lafadz yang menunjukan makna khulu’ seperti kata mubara’ah (melepas diri) atau fidyah (tebusan). Jika tidak dengan lafadz khulu’ atau lafadz yang
Jenis penelitian yang digunakan dalam penelitian ini adalah penelitian quasi experiment atau penelitian eksperimen semu untuk menguji hipotesis adakah dampak