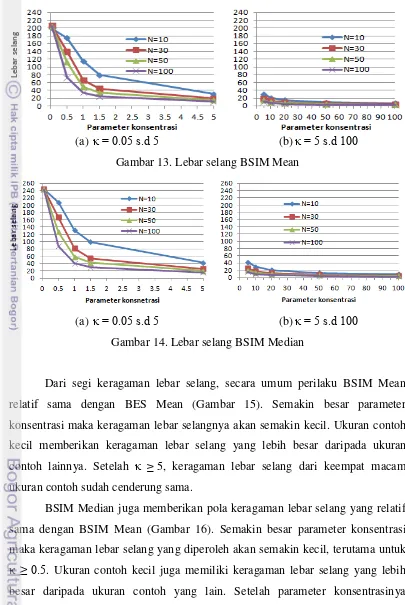
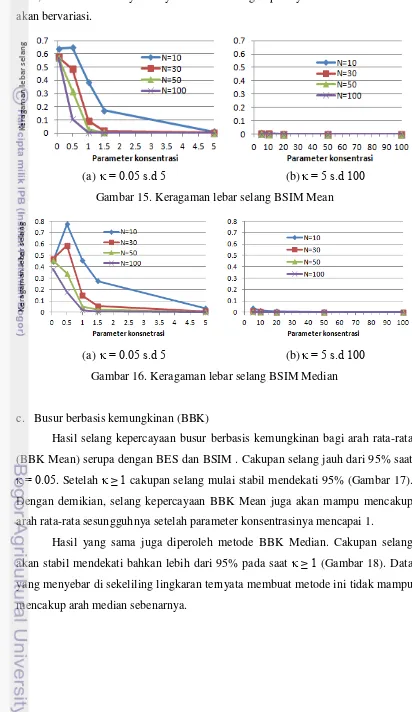
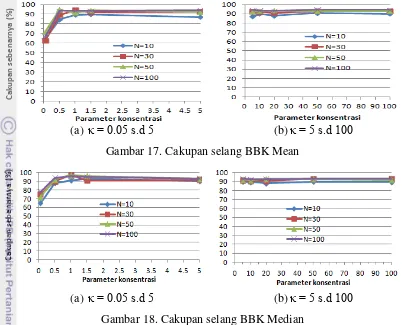
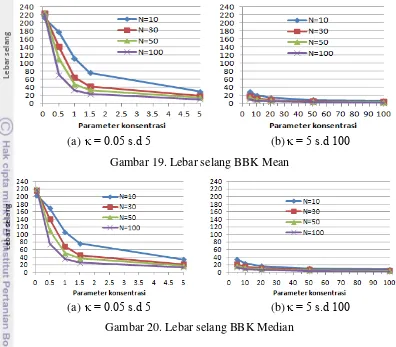
Bootstrap Confidence Interval Estimation of Preferred Direction for Circular Data
Teks penuh
Gambar


Dokumen terkait
Pertama, jika reaksi energi tinggi yang melibatkan ensim sitokrom p-450 menyebabkan ikatan kovalen obat dengan protein intrasel, maka akan terjadi disfungsi
f. Mahasiswa berkonsultasi kepada pembimbing yang telah ditunjuk dalam menyusun laporan studi kasus yang dilakukan dengan cara online. Mahasiswa mengisi format
24 Penggunaan perbedaan temporer yang boleh dikurangkan pada masa yang akan datang terjadi dalam bentuk pengurangan laba fiskal. Namun, manfaat ekonomi berupa pengurangan
Indosat, Tbk di Indonesia melalui analisis peramalan sebagai landasan perencanaan pemasaran, (2) Mengetahui apakah program dan paket Matrix BlackBerry yang ditawarkan mampu
Fungsi Pelaksana sebagaimana dimaksud dalam Pasal 8 merupakan fungsi Pelaksana BPBD dilaksanakan secara terkoordinasi dan terintegrasi dengan satuan kerja perangkat
Kombinasi yang baik dari elemen-elemen yang mendukung dapat menciptakan brand image yang kuat bagi konsumen.Citra merek menjadi hal yang sangat penting diperhatikan
Selain itu, aplikasi ini juga dapat membantu mereka untuk mendapatkan bahan renungan yang diberikan dalam bentuk website rohani tanpa perlu menghafalkan alamat
pembangunan dan pelayanan kepada masyarakat di daerah, Pemerintah Kabupaten Bangka Selatan memerlukan dokumen perencanaan pembangunan jangka menengah demi mewujudkan