On the Markowitz mean variance analysis
Teks penuh
Gambar
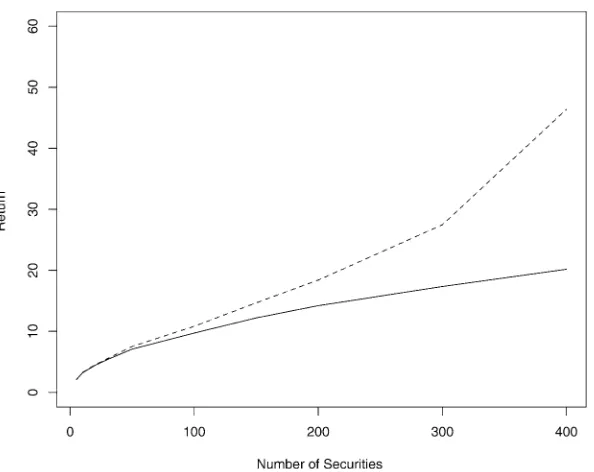
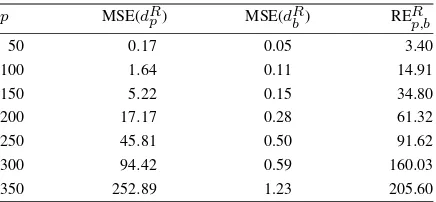
Garis besar
Dokumen terkait
Penelitian ini adalah tentang Pengaruh Keadilan pajak dan Sanksi Perpajakan Terhadap Kepatuhan Wajib Pajak Dengan Kualitas Pelayanan Sebagai Variabel Moderating..
Selanjutnya, untuk menilai apakah perusahaan kontraktor sudah menerapkan prinsip GCG dengan baik maka penulis menggunakan teknik penilaian dengan metode skoring
Keluaran Jumlah pakaian peringatan hari-hari tertentu 25 stel Hasil Persentase cakupan layanan peningkatan
Hasil penelitian menunjukkan bahwa kepuasan social benefits dan structural ties memiliki pengaruh positif dan signifikan terhadap loyalitas pelanggan dengan kepuasan
Agar manajemen dapat melakukan perencanaan, pengendalian dan pengambilan keputusan tentang mutu produk, manajemen perlu mematuhi pengertian biaya mutu ( cost of
Klinik PT POS Indonesia merupakan suatu instansi kesehatan yang bergerak pada pelayanan jasa kesehatan dan penjualan obat, dalam kegiatan pelayanannya tersebut Kelinik ini
Menghapus node pada AVL Tree sama dengan menghapus binary search tree procedure dengan perbedaan pada penanganan kondisi tidak balance. Penanganan kondisi tidak balance
[r]