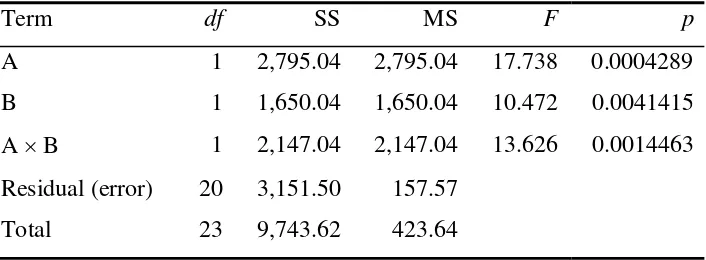
Analysis of variance
Teks penuh
Gambar
Garis besar
Dokumen terkait
Pengaruh Penerapan Strategi Pembelajaran Think – Talk - Write (TTW) dan Minat Belajar terhadap Kemampuan Menulis Puisi Pada Siswa Kelas.. VIII SMP Swasta Dharma Pancasila Medan
[r]
Bagi para penyedia jasa pemborongan yang berminat mengikuti pelelangan tersebut, dapat mendaftarkan perusahaannya kepada Panitia Pengadaan di Kantor Balai Konservasi Sumber Daya Alam
Pertama : Menunjuk Tiem Badan Pertimbangan Jabatan dan Kepangkatan Kantor Kementerian Agama Kabupaten Soppeng dengan susunan personalia sebagaimana tersebut dalam kolom
Mengingat bahan baku minyak dengan kandungan asam lemak tinggi jika digunakan sebagai bahan baku pada reaksi transesterifikasi yang berkatalis basa, maka asam
mengandung sel-sel dari strain-strain efektif mikroba penambat nitrogen, pelarut fosfat atau selulolitik yang digunakan pada biji, tanah atau tempat pengomposan
PERAN IKLAN TELEVISI LAYANAN MASYARAKAT SEBAGAI PENYEBAR PERUBAHAN TATACARA PEMILU LEGISLATIF DENGAN PENGETAHUAN PEMIRSA.. Kasus: Masyarakat Desa Cihideung Ilir,
―pengaruh likuiditas, leverage, profitabilitas, kualitas audit, dan opini audit tahun sebelumny terhadap penerimaan opini audit going concern pada perusahaan pertambangan