SYARAT CUKUP UNTUK MEMINIMALKAN PENYEBARAN PENYAKIT TUBERCULOSIS PADA SUATU KOMUNITAS
Teks penuh
Gambar
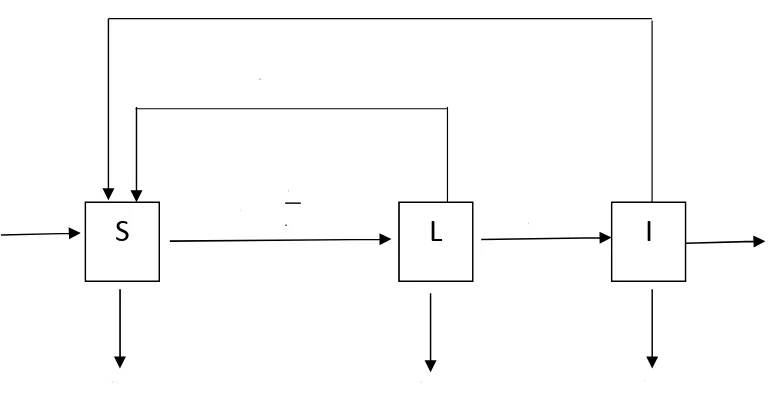
Dokumen terkait
ten korvaajiksi kehitettiin sekulaareja vastineita, sillä haluttiin murtaa kirkon monopoli ihmi- sen elämänkaaren taitekohtien juhlissa. Vuonna 1957 järjestettiin ensimmäiset
Berdasarkan Latar Belakang Masalah, permasalahan yang yang akan diangkat pada penelitian ini adalah bagaimana membangun aplikasi E-Commerce untuk transaksi produk
Darmini. Program Studi Pendidikan Ekonomi Akuntansi. Fakultas Keguruan dan Ilmu Pendidikan, Universitas Muhammadiyah Surakarta, 2012. Tujuan dari penelitian ini adalah untuk
Kedua, perubahan status permodalan Perseroan Terbatas Penanaman Modal Asing menjadi Perseroan Terbatas Penanaman Modal Dalam Negeri tidak diatur dalam peraturan manapun
a. pimpinan auditi atas rekomendasi hasil audit dan reviu lainnya; b. memberitahukan langkah-langkah yang harus dilakukan auditi agar tindak lanjut hasil audit bisa
Penelitian ini bertujuan mengidentifikasi kualitas pedestrian menuju ruang terbuka di perumahan, mengidentifikasi kualitas linkage di perumahan, dan mengetahui
semua proses finishing selesai, maka barang tersebut akan diberikan pada bagian pengiriman beserta dengan nota rangkap 1 dan rangkap 2. Jika
Bagian Jurnal releksi dapat dijadikan alat untuk menuntun siswa dalam menemukan makna pada pelajaran kimia karena proses pengerjaan jurnal refleksi melibatkan