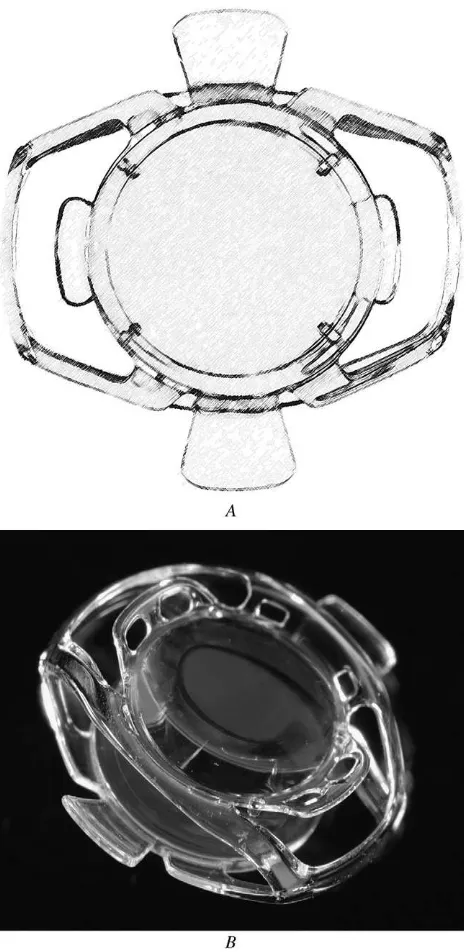
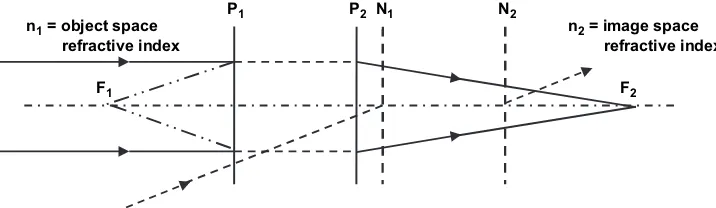
Synchrony dual optic accommodating intra 001
Teks penuh
Gambar


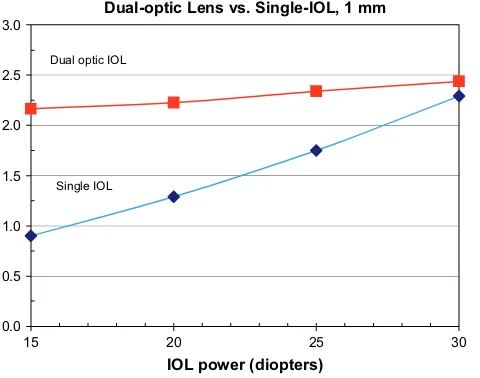
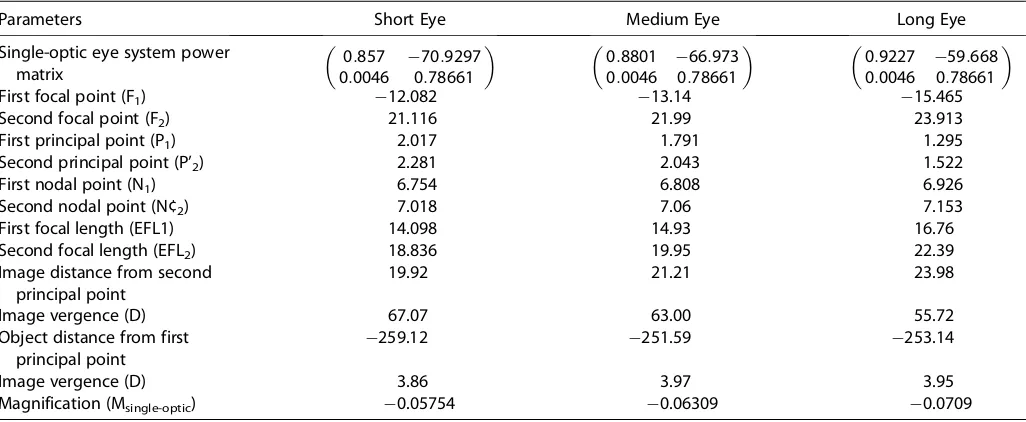
Garis besar
Dokumen terkait
Setelah melakukan analisa data pada penelitian, maka selanjutnya yaitu memaparkan hasil penelitian tersebut dalam bentuk tabel yang menggambarkan perbedaan hasil
Nipah Panjang Kabupaten Tanjung Jabung Timur Tahun Anggaran 2015, untuk Paket Pekerjaan tersebut diatas telah dilaksanakan Pembukaan Penawaran pada Tanggal 12 November 2015,
Nama Lelang Kajian Pengembangan Potensi Wisata Kecamatan Kuala Jambi Kabupaten Tanjung Jabung Timur(Lelang Ulang) Nilai Pagu Paket Rp 97.800.000,00 Nilai HPS Paket
Masing-masing kelompok kemudian diberi 3 masalah matematika yang diselesaikan dengan membuat model matematikanya terlebih dahulu. Penelitian ini dilakukan dalam satu kali
XXII Author Index/Journal of Insect Physiology 46(2000) XVIII–XXII.
The Whozin Email Program pays you to read your own emails Word Count:..
Dari selisih data (point) yang telah didapat maka dapat diambil kesimpulan untuk short circuit turn 1 pada fasa R- Ground pada gambar 12 perubahan selisih beda fasa
Undang-Undang Nomor 32 Tahun 2004 tentang Pemerintahan Daerah (Lembaran Negara Republik Indonesia Tahun 2004 Nomor 125, Tambahan Lembaran Negara Republik Indonesia Nomor