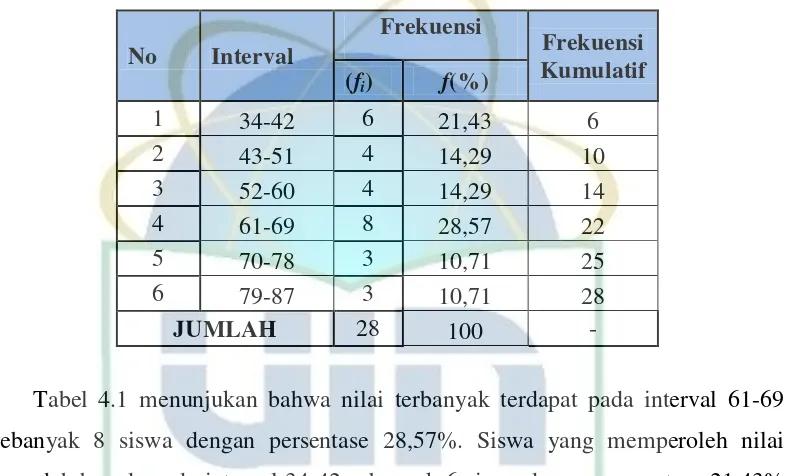
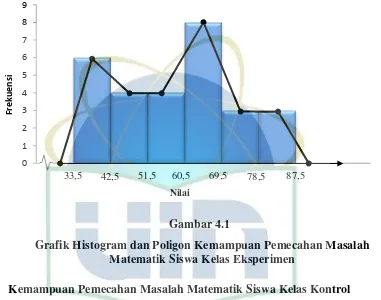
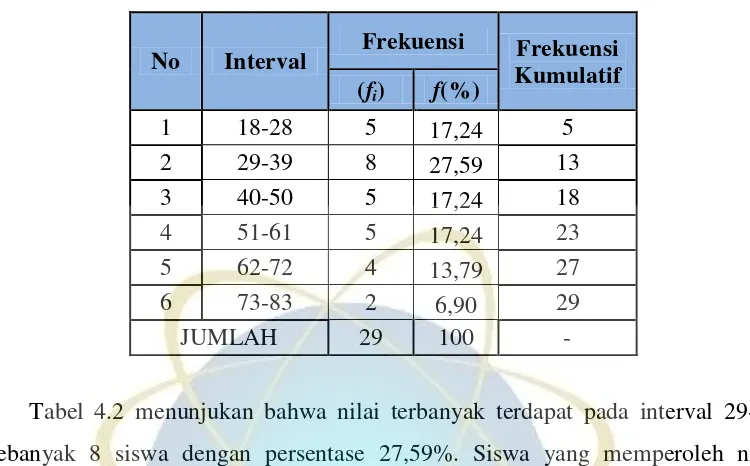
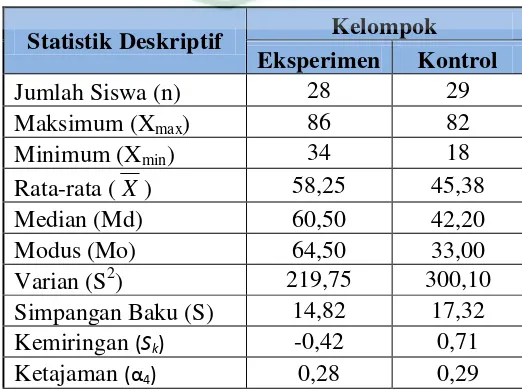
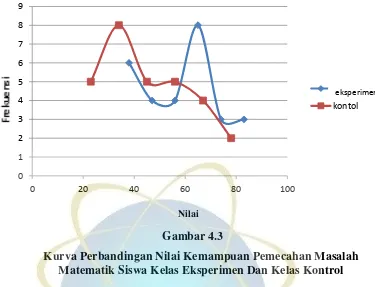
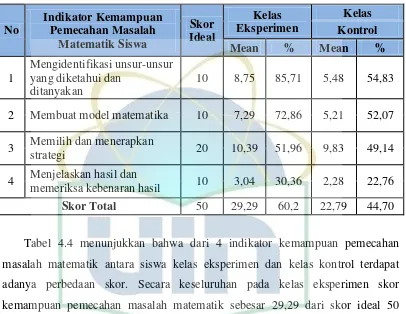
Pengaruh model process oriented guided inquiry learning (pogil) terhadap kemampuan pemecahan masalah matematik siswa
Teks penuh
Gambar




Dokumen terkait
Dalam rangka pengisian Jabatan Pimpinan Tinggi Pratama Pemerintah Kabupaten Muaro Jambi Jambi Tahun 2017, sesuai dengan Peraturan Pemerintah Nomor 11 Tahun 2017 tentang
Menurut Husein & Pambekti (2014) hal lain yang dapat kita lihat pada model Zmijewski adalah bahwa model Zmijewski menekankan besarnya utang dalam memprediksi
Rencana yang dirancang untuk mencapai tujuan organisasi yang lebih luas :.. Menurut Peter Drucker, seorang manajer dalam setiap operasinya lebih
Pejabat Pengadaan pada Kegiatan Pengembangan Kawasan Budidaya Air Payau, telah melaksanakan Proses Evaluasi Kualifikasi dan Penawaran dalam Pengadaan Langsung untuk
a. Dosen wajib bekerjasama dengan manajemen yayasan pendidikan / lembaga resmi penyelenggara pendidikan , instansi pemerintah melalui Departemen Pendidikan Nasional
Disebabkan keadaan kawasan kajian yang agak jauh dan sekiranya ianya ingin melaksanakan kajian dengan merangkumi 4 perkampungan ini, ianya akan mengambil masa
KARAKTER: Jika bermaksud memancingnya (biasanya sebagai umpan untuk ikan yang lebih besar), peralatan yang paling baik adalah piranti jenis.. Spinning dengan umpan
[r]