ANALISIS KEMAMPUAN BERPIKIR KREATIF MATEMATIS SISWA SMP
Teks penuh
Gambar
Dokumen terkait
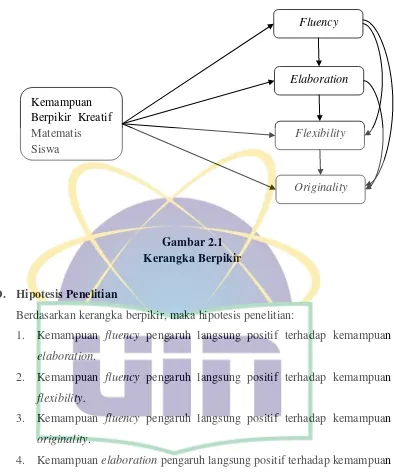
Penelitian ini bertujuan untuk mendeskripsikan kemampuan berpikir kreatif matematis pada indikator fluency, flexibility, dan originality dalam menyelesaikan soal
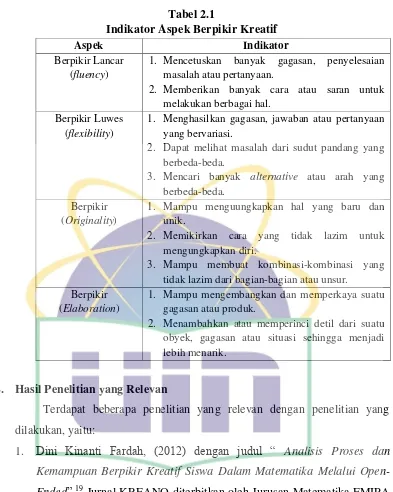
1) Berpikir lancar (fluent thinking) atau kelancaran adalah kemampuan memproduksi banyak gagasan. Siswa dapat memberikan banyak gagasan, jawaban, penyelesaian masalah
Kunci Jawaban Pretest Kemampuan Berpikir Kreatif Matematis Kunci Jawaban Posttest Kemampuan Berpikir Kreatif Matematis Kisi-Kisi Angket Kemandirian Belajar Siswa.. Angket
Siswa dengan self concept tinggi dapat menggunakan semua indikator kemampuan berpikir kreatif matematis dengan maksimal, mampu memenuhi empat aspek kemampuan
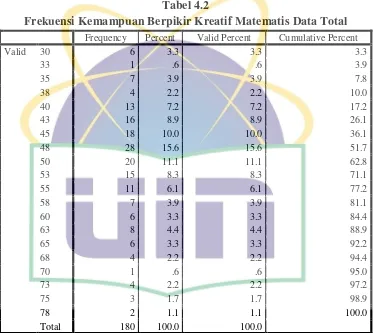
Dilihat dari tabel 2, dari keseluruhan siswa menjawab soal kemampuan berpikir kreatif tersebut, didapatkan kesimpulan bahwa semua siswa tergolong kedalam kriteria cukup
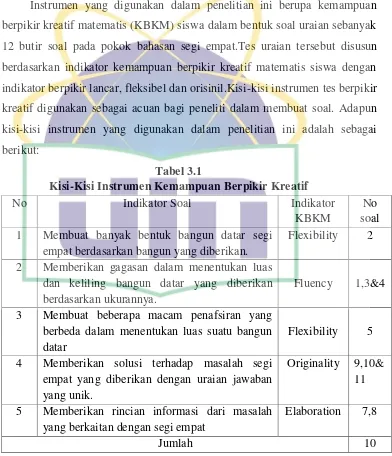
Pengembangan instrumen penilaian kemampuan berpikir kreatif matematis adalah pengembangan instrumen atau alat ukur yang digunakan untuk mengukur kemampuan berpikir kreatif
Berdasarkan analisis data, diperoleh bahwa kemampuan berpikir kreatif matematis siswa dalam menyelesaikan soal open-ended pada aspek berpikir lancar (fluency)
Sedangkan pada jawaban siswa yang memiliki self-regulated learning kurang baik, tidak dapat menyelesaikan tes kemampuan berpikir kreatif matematis dengan baik.. Berikut