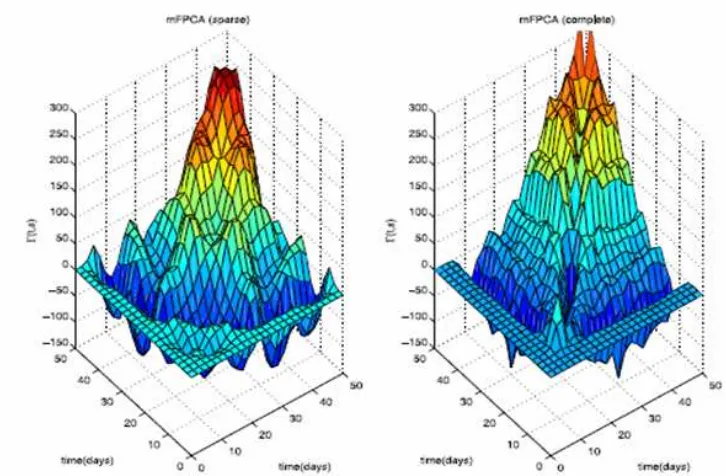
Kovariat Dari Fungsional Prinsipal Komponen Analisis Untuk Data Longitudinal
Teks penuh
Gambar
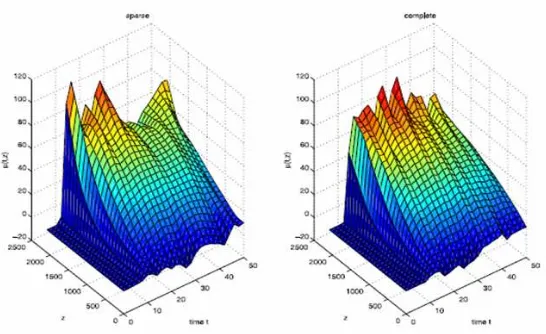
Dokumen terkait
Perencanaan pembelajaran membaca tembang macapat sesuai titi laras dibuat oleh guru Bahasa Indonesia SMP Negeri 2 Kras Kabupaten Kediri, mencakup (1) identitas
Bullying merupakan salah satu permasalahan yang terjadi pada remaja yang tidak hanya berampak terhadap harga diri saja tetapi juga terhadap pendidikan, kesejahteraan
depresiasi dan amortisasi , jumlah ini menunjukan jumlah modal kerja yang berasal dari hasil operasi perusahaan. Jadi jumlah modal kerja yang berasal dari hasil
Lignin tidak dapat dicerna oleh mikroba didalam rumen, bahkan dapat mengganggu kecernaan, sedangkan serat kasar memiliki fraksi selain lignin juga mengandung selulosa
Tujuan sistem informasi akutansi adalah untuk menyediakan informasi yang diperlukan dalam pengambilan keputusan yang dilaksanakan oleh aktivitas yang disebut
Penelitian ini dilakukan untuk mengetahui pengaruh pemberian ekstrak jaloh (Salix tetrasperma Roxb) pada ayam pedaging yang diberi cekaman panas pada suhu 33 ± 1 o C selama 4 jam
Untuk mewujudkan visi tersebut, Deputi Bidang Operasi SAR mempunyai misi yaitu “Merumuskan kebijakan dalam rangka penyelenggaraan kegiatan operasi SAR yang efisien dan
Berdasarkan hasil penelitian dapat disimpulkan yaitu: (1) terdapat perbedaan rapat arus yang signifikan dari sampel sedimen, namun perbedaan tersebut disebabkan oleh sampel