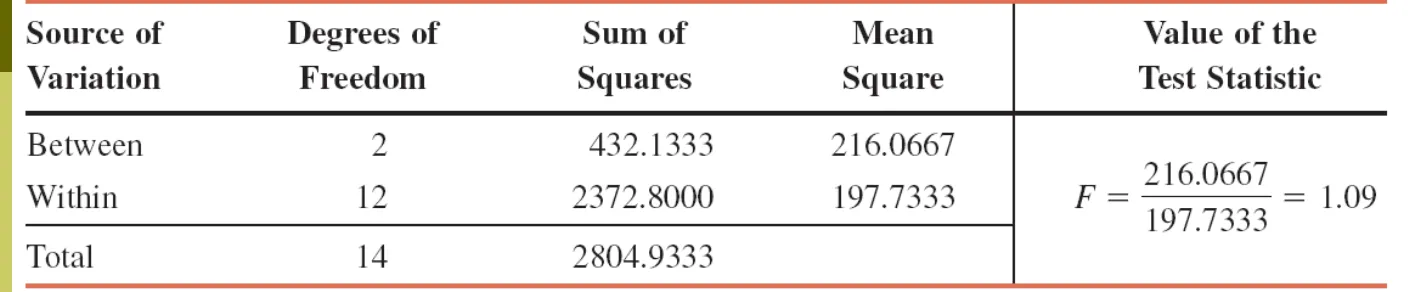
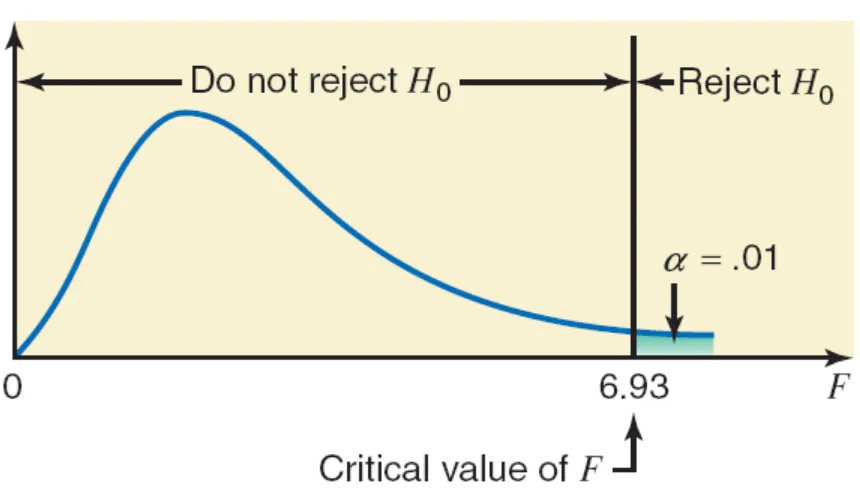
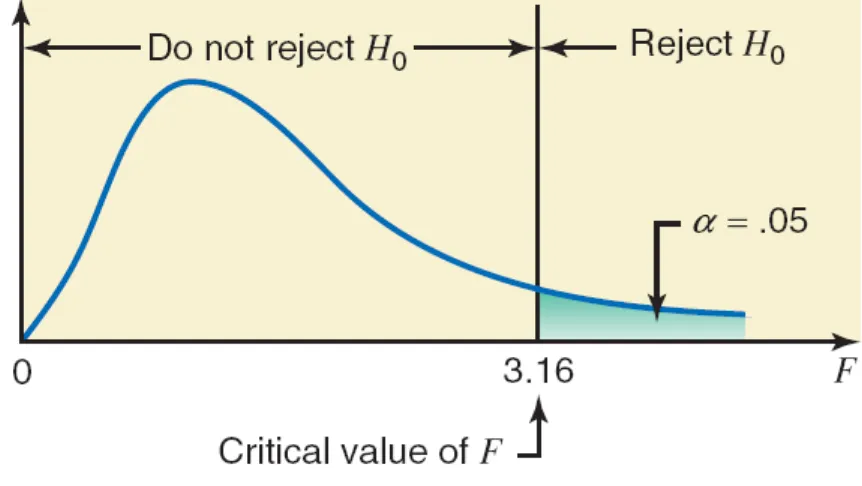
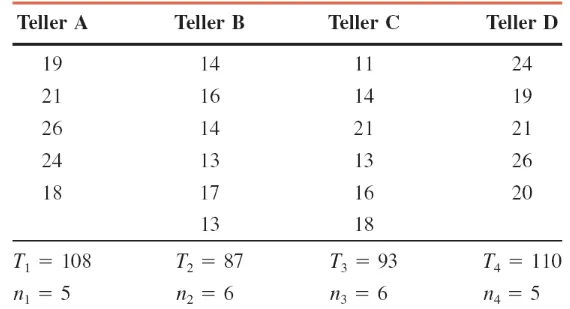
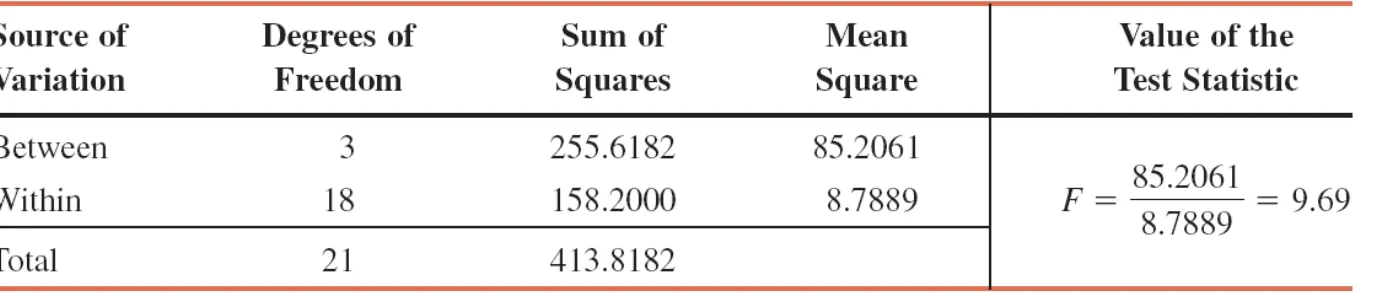
ANALYSIS OF VARIANCE 001
Teks penuh
Gambar
Garis besar
Dokumen terkait
tahapan pertama yang akan dituangkan ke dalam Rencana Pembangunan.. Jangka Menengah Daerah ( RPJMD ) Tahun 2008
Apabila ada yang berkeberatan terhadap pengumuman ini, dapat mengajukan sanggahan yang ditujukan kepada Panitia Pengadaan Barang/Jasa Kantor Wilayah BPN Provinsi
BPR Mentari Terang Tuban, hasil penelitian ini menunjukkan bahwa faktor kualitas kerja yang terdiri dari variabel restrukturisasi kerja, sistem imbalan, dan
universitas dalam mengembangkan SI/TI di UDLS Manado yang searah dengan. strategi universitas dengan menggunakan metodologi
PELAKSANAAN PEMBERIAN KESEMPATAN KERJA BAGI PEKERJA PENYANDANG DISABILITAS DI PT.ALFA RETAILINDO (CARREFOUR)..
Yang menghadir i adalah dir ektur per usahaan atau boleh diw akilkan kepada pengur us lain yang namanya ter cantum dalam Akte Notar is Pendir ian atau Per ubahan dengan
Panduan Lengkap Kelapa Sawit: Manajemen Agribisnis dari Hulu.
Sejalan dengan kebijakan pemerintah itu, Hankuk University of Foreign Studies (HUFS) dan sejumlah per- guruan tinggi terdepan di Korea Selatan mulai menyelenggarakan kebijakan