Optimasi Parameter Pemesinan Pada Mesin Sekrap Model L-450 Menggunakan Algoritma Genetika
Teks penuh
Gambar


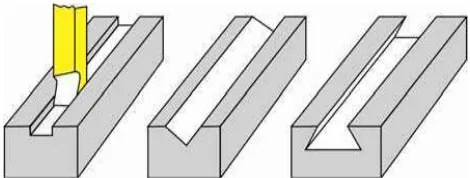
![Gambar 2.6 Bentuk Pahat Sekrap [11]](https://thumb-ap.123doks.com/thumbv2/123dok/71056.7143/34.595.267.373.597.720/gambar-bentuk-pahat-sekrap.webp)
Dokumen terkait
Terdapat tiga pengujian yang dilakukan dalam pengujian ini yaitu pengujian yang akan dilihat dari hasil nilai fitness paling optimal, sehingga dapat ditemukan
Pada algoritma genetika mampu mendapatkan nilai parameter optimal secara otomatis pada klasifikasi FAMB dengan tingkat akurasi yang lebih tinggi untuk set data
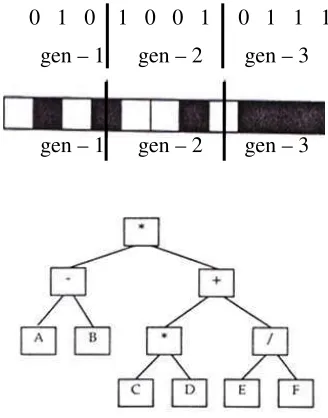
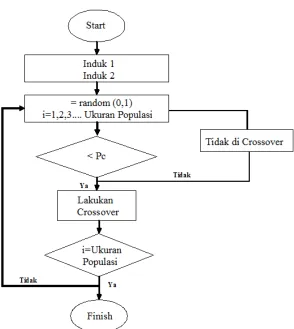
z Permasalahan dengan parameter yang jumlah dan range nilainya tertentu sebaiknya menggunakan bentuk kromosom biner, seperti mencari nilai. optimal
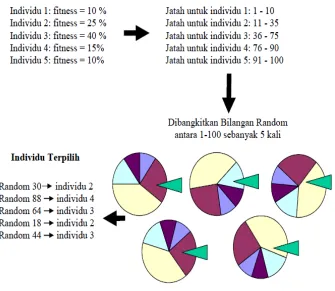
Sebab Seleksi dilakukan secara acak, sehingga tidak ada jaminan bahwa krosomom yang memiliki nilai fitness yang terbaik yang akan dipilih, bisa juga nilai fitness
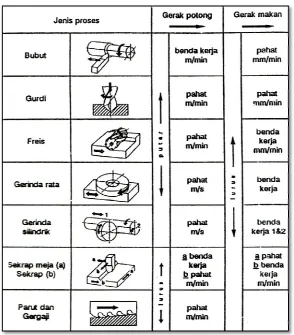
fungsi optimasi yang digunakan adalah waktu pemesinan (t c ) maka dipilih.. pengerjaan dengan waktu paling singkat, sehingga didapat hasil
Berdasarkan ketiga uji coba yang telah dilakukan terhadap setiap parameter algoritma genetika, maka diperoleh titik optimal untuk memperoleh nilai fitness terbaik,
Berdasarkan ketiga uji coba yang telah dilakukan terhadap setiap parameter algoritma genetika, maka diperoleh titik optimal untuk memperoleh nilai fitness terbaik,
Terdapat tiga pengujian yang dilakukan dalam pengujian ini yaitu pengujian yang akan dilihat dari hasil nilai fitness paling optimal, sehingga dapat ditemukan